
分析 (1)椭圆的焦点在x轴上,经过P(0,2),即b=2,由离心率公式e=$\frac{c}{a}$,及a2=b2+c2,即可a和c的值,即可求得椭圆方程;
(2)假设存在直线,将直线方程代入椭圆方程,消去y得到关于x的一元二次方程,设出M和N点坐标及MN的中点坐标,由韦达定理可知,即可求得A点坐标,判断当k=0时,成立,当k≠0.,求得直线AP的斜率,由MN⊥AP,得-$\frac{9{k}^{2}+5}{6k}$•k=-1,即可求得k的值.
解答 解:(1)∵椭圆C经过点P(0,2),
∴b=2,
离心率e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$.即a2=$\frac{3}{2}$c2=$\frac{3}{2}$(a2-b2),整理得a2=3b2=12,
∴$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1$.
(2)假设存在直线l满足条件,则:$\left\{\begin{array}{l}{y=kx-\frac{4}{3}}\\{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,消去y整理得:(1+3k2)x2-8kx-$\frac{20}{3}$=0,△>0恒成立,
设M(x1,y1),N(x2,y2),设A(x0,y0)为线段MN的中点,则,
x1+x2=$\frac{8k}{1+3{k}^{2}}$,x0=$\frac{4k}{1+3{k}^{2}}$,y0=kx0-$\frac{4}{3}$=-$\frac{4}{3(1+3{k}^{2})}$,即A($\frac{4k}{1+3{k}^{2}}$,-$\frac{4}{3(1+3{k}^{2})}$),
当k=0时,满足题意,
当k≠0时,直线AP的斜率kAP=$\frac{-\frac{4}{3(1+3{k}^{2})}-2}{\frac{4k}{1+3{k}^{2}}}$=-$\frac{9{k}^{2}+5}{6k}$,
由MN⊥AP,得-$\frac{9{k}^{2}+5}{6k}$•k=-1,解得:k=±$\frac{1}{3}$,
故直线的斜率为:k=0,$\frac{1}{3}$,-$\frac{1}{3}$.
点评 本题考查椭圆的标准方程和简单性质,中点公式、韦达定理及斜率公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
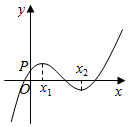
| A. | φ(1)<0 | B. | φ(1)>0 | C. | φ(1)≤0 | D. | φ(1)=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com