
(本小题满分12分)在如图所示的平面直角坐标系中,已知点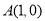 和点
和点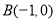 ,
, ,且
,且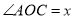 ,其中
,其中 为坐标原点.
为坐标原点.
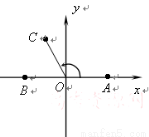
(1)若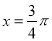 ,设点
,设点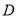 为线段
为线段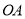 上的动点,求
上的动点,求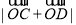 的最小值;
的最小值;
(2)若 ,向量
,向量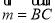 ,
,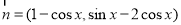 ,求
,求 的最小值及对应的
的最小值及对应的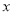 值.
值.
(1)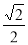 ;(2)
;(2)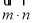 的最小值为
的最小值为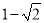 ,此时
,此时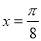
【解析】
试题分析:(1)向量的坐标运算主要是利用加、减、数乘运算法则进行的,若已知有向线段两端点的坐标,则应先求出向量的坐标,解题过程中要注意方程的思想应用级运算法则的正确使用,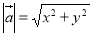 ;(2)先用数量积的概念转化为三角函数的形式,寻求角与角之间的关系,化非特殊角为特殊角;正确灵活运用公式,通过三角变换消去或约去一些非特殊角的三角函数值,注意题中角的范围;(3)掌握一些常规技巧:“1”的代换,和积互化等,异名三角函数化为同名三角函数,异角化为同角,异次化为同次,切化弦,特殊角与特殊角的三角函数互化;(4)注意利用转化的思想,本题转化为求最值,熟悉公式的整体结构,体会公式间的联系,倍角公式和辅助角公式应用是重点.
;(2)先用数量积的概念转化为三角函数的形式,寻求角与角之间的关系,化非特殊角为特殊角;正确灵活运用公式,通过三角变换消去或约去一些非特殊角的三角函数值,注意题中角的范围;(3)掌握一些常规技巧:“1”的代换,和积互化等,异名三角函数化为同名三角函数,异角化为同角,异次化为同次,切化弦,特殊角与特殊角的三角函数互化;(4)注意利用转化的思想,本题转化为求最值,熟悉公式的整体结构,体会公式间的联系,倍角公式和辅助角公式应用是重点.
试题解析:【解析】
(Ⅰ) 设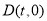 (
(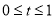 ),又
),又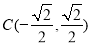
所以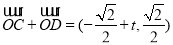
所以 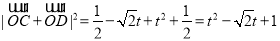
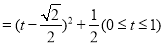
所以当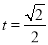 时,
时,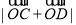 最小值为
最小值为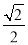
(Ⅱ)由题意得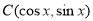 ,
,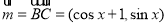
则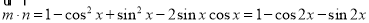
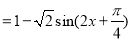
因为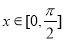 ,所以
,所以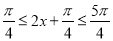
所以当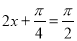 ,即
,即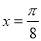 时,
时,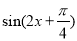 取得最大值
取得最大值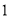
所以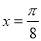 时,
时, 取得最小值
取得最小值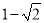
所以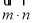 的最小值为
的最小值为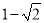 ,此时
,此时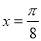
考点:1、求向量的模;2、三角函数的化简;3、求三角函数的最值.


科目:高中数学 来源:2015届湖北省襄阳市高三阶段性测试数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数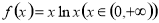 .
.
(1)求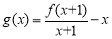
 的单调区间与极大值;
的单调区间与极大值;
(2)任取两个不等的正数 ,且
,且 ,若存在
,若存在 使
使 成立,求证:
成立,求证: ;
;
(3)已知数列 满足
满足 ,
, (n∈N+),求证:
(n∈N+),求证: (
( 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源:2015届湖北省襄阳市高三阶段性测试数学试卷(解析版) 题型:选择题
按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数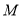 的值是( )
的值是( )
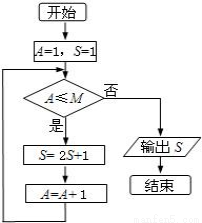
A.5 B.6 C.7 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com