
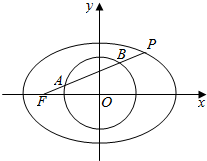
 如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P,若FA=PB,且AB=$\frac{\sqrt{3}a}{2}$,则椭圆的离心率为$\frac{\sqrt{10}}{4}$.
如图,过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P,若FA=PB,且AB=$\frac{\sqrt{3}a}{2}$,则椭圆的离心率为$\frac{\sqrt{10}}{4}$. 分析 由题意画出图形,得到焦点三角形为直角三角形,利用平面几何知识求得PF、PG的长度,结合勾股定理求得答案.
解答 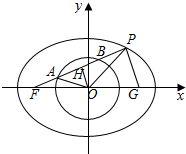 解:如图,
解:如图,
设椭圆的右焦点为G,连接PG,
∵FA=PB,取FP中点H,连接OH,则OH⊥PF,
∴可得PF⊥PG,
∵AB=$\frac{\sqrt{3}a}{2}$,∴AH=$\frac{\sqrt{3}a}{4}$,
圆x2+y2=$\frac{{a}^{2}}{4}$的半径OA=$\frac{a}{2}$,∴OH=$\sqrt{O{A}^{2}-A{H}^{2}}=\sqrt{(\frac{a}{2})^{2}-(\frac{\sqrt{3}a}{4})^{2}}$=$\frac{a}{4}$.
∴FH=$\sqrt{{c}^{2}-(\frac{a}{4})^{2}}$,则PF=$2\sqrt{{c}^{2}-\frac{{a}^{2}}{16}}$,
则$PG=2a-2\sqrt{{c}^{2}-\frac{{a}^{2}}{16}}$.
∴$4({c}^{2}-\frac{{a}^{2}}{16})+(2a-2\sqrt{{c}^{2}-\frac{{a}^{2}}{16}})^{2}=4{c}^{2}$,
整理得:64e4-144e2+65=0,解得${e}^{2}=\frac{13}{8}$(舍)或${e}^{2}=\frac{5}{8}$,
则$e=\frac{\sqrt{10}}{4}$.
故答案为:$\frac{\sqrt{10}}{4}$.
点评 本题考查直线与圆锥曲线的综合问题.考查数形结合的解题思想方法和数学转化思想方法,由题意得到焦点三角形为直角三角形是解决本题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4$\overrightarrow{a}$-2$\overrightarrow{b}$ | B. | 4$\overrightarrow{a}$+2$\overrightarrow{b}$ | C. | -2$\overrightarrow{a}$+4$\overrightarrow{b}$ | D. | 2$\overrightarrow{a}$+4$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
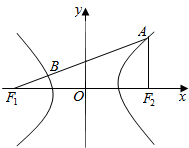 已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.
已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [1,4) | C. | [1,2] | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 12 | C. | 24 | D. | 4|m| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com