
如图直角梯形CBHQ,CB=2,BH=4,HQ=3,BH的中点为原点O,一曲线过Q点且曲线上任意一点到B、H的距离之和都相等.
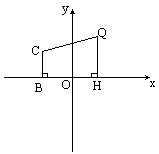
(1)求曲线方程;
(2)设曲线上任意一点P,求∠BPH的范围;(3)曲线上的弦以C为中点的有几条?并证明你的结论.
|
解(1)由题意曲线为椭圆,且过Q点
∵BH=4 O为中点 ∴c=2 又∵QB+QH=8 ∴a=4 解(2)设曲线上任意一点P 则|PB|+|PH|=8 又cosθ= ∵cosθ在[0,π]上单调递减 ∴θ∈[0, 解(3)有一条 证明:设过C(-2,2)的直线斜率为k. 当k=0和k不存在时,C不是弦的中点, 再设过C的直线方程为y=k(x+2)+2 代入椭圆方程 得(3+4k2)x2+16k(1+k)x+16(1+k)2-12×4=0 ∵3+4k2≠0 ∴ 有唯一解. ∴仅有一条弦 (法二反证法) |


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:2007年高考数学理科综合实战演练试卷二 人教版 人教版 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2007届广东省韶关市高三摸底考试数学(文)试题 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:龙门中学、新丰一中、连平中学三校联考试题、高三数学(理) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2007龙门中学、新丰一中、连平中学三校联考试题、高三数学(文) 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com