
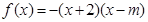 (其中
(其中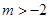 ).
).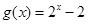 .
.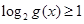 ”是假命题,求
”是假命题,求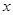 的取值范围;
的取值范围;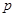 :
: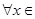
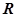 ,
,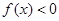 或
或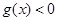 ;命题
;命题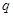 :
: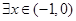 ,
,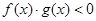 .若
.若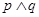 是真命题,求
是真命题,求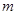 的取值范围.
的取值范围.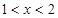 ;(2)
;(2)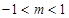 .
.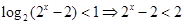 ”这里错在不是等价转化,切记去掉对数符号后一定要保证真数为正;(2)解决此问题,对逻辑分析问题的能力要求比较高,首先要掌握逻辑用语的知识,然后还需借助集合的语言来描述,最终回到不等式求解,且需关注细节:端点是否带等号,这样才能善始善终.
”这里错在不是等价转化,切记去掉对数符号后一定要保证真数为正;(2)解决此问题,对逻辑分析问题的能力要求比较高,首先要掌握逻辑用语的知识,然后还需借助集合的语言来描述,最终回到不等式求解,且需关注细节:端点是否带等号,这样才能善始善终.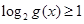 ”是假命题,则
”是假命题,则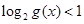 , 2分
, 2分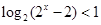 ,
,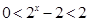 ,解得
,解得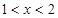 5分
5分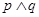 是真命题,则
是真命题,则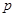 和
和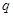 都为真命题. 6分
都为真命题. 6分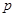 是真命题,则
是真命题,则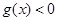 的解集的补集是
的解集的补集是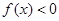 解集的子集;
解集的子集;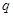 是真命题,则
是真命题,则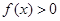 的解集与
的解集与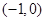 的交集非空.
的交集非空.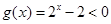 ,则
,则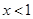 .
.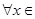
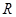 ,
, 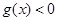 或
或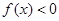 ,
,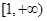 是
是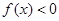 的解集的子集.
的解集的子集.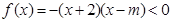 (其中
(其中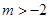 ),解得得
),解得得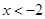 或
或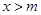 ,
,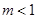 . 9分
. 9分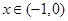 时,
时,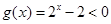 ,
,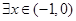 ,使得
,使得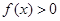 ,
,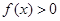 的解集与
的解集与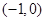 的交集非空.
的交集非空.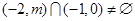 ,则
,则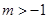 , 13分
, 13分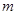 的取值范围是
的取值范围是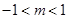 14分
14分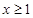 时,
时,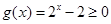 ,因为
,因为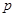 是真命题,则
是真命题,则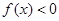 ,
,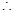
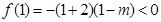 ,即
,即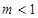 9分
9分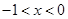 时,
时,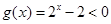 ,因为
,因为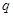 是真命题,则
是真命题,则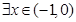 ,使
,使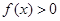 ,
,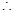
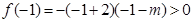 ,即
,即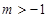 13分
13分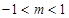 . 14分
. 14分

科目:高中数学 来源:不详 题型:单选题
| A.命题“?x∈R,ex>0”的否定是“?x∈R,ex>0” |
| B.命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 |
| C.“x2+2x≥ax在x∈[1,2]上恒成立”?“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立” |
| D.命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 2 |
| 1-i |
| . |
| z |
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| α |
| β |
| α |
| β |
| α |
| 0 |
| β |
| 0 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| lim |
| n→∞ |
| π |
| 2 |
| A.①② | B.②③ | C.①④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.命题“若x2 =4,则x=2”的否命题为:“若x2 =4,则x≠2” |
| B.“x=2”是“x2—6x+8=0”的必要不充分条件 |
| C.命题“若x=y,则cosx=cosy”的逆否命题为真命题 |
| D.命题“存在x∈R,使得x2+x+3>0”的否定是:“对于任意的x∈R,均有x2 +x+3<0" |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.?x∈R,ex≤0 |
| B.?x∈R,2x>x2 |
C.a+b=0的充要条件是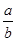 =-1 =-1 |
| D.a>1,b>1是ab>1的充分条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
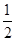 ,
,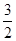 ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com