已知函数f(x)的定义域为(0,+∞),对任意正数x1,x2均有f(x1x2)=f(x1)+f(x2).
(Ⅰ)请写出一个这样的函数f(x);
(Ⅱ)若x>1时,f(x)>0,判断f(x)在(0,+∞)上的单调性,并加以证明.你还能发现f(x)的其他性质吗?
【答案】
分析:(Ⅰ)结果不唯一,如f(x)=0(x>0),f(x)=log
2x等.
(Ⅱ)可类比对数函数提出猜想:f(x)在(0,+∞)上是增函数,再利用定义证明即可.
解答:解:(Ⅰ)∵函数f(x)的定义域为(0,+∞),对任意正数x
1,x
2均有f(x
1x
2)=f(x
1)+f(x
2),
∴f(x)=0(x>0)就是这样的函数(也可用f(x)=log
2x).
(Ⅱ)类比对数函数提出猜想:f(x)在(0,+∞)上是增函数.
证明:设0<x
1<x
2,则
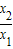
>1,
∵x>1时,f(x)>0,
∴f(
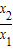
)>0,
∴f(x
2)-f(x
1)=f(x
1•
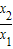
)=f(x
1)+f(
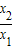
)-f(x
1)=f(
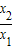
)>0,
∴f(x
1)<f(x
2),
∴f(x)在(0,+∞)上是增函数(证毕).
f(x)还具有下列性质:f(x)的图象经过(1,0);当0<x<1时,y<0.
点评:本题考查抽象函数及其应用,突出考查函数单调性的判断与证明,考查转化思想与运算能力,属于中档题.

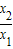 >1,
>1,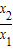 )>0,
)>0,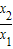 )=f(x1)+f(
)=f(x1)+f(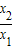 )-f(x1)=f(
)-f(x1)=f(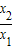 )>0,
)>0,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案