
| A. | (-∞,$\frac{1}{2}$) | B. | (-1,$\frac{1}{2}$) | C. | [-$\frac{2}{5}$,$\frac{1}{2}$) | D. | [-$\frac{2}{5}$,+∞) |
分析 利用向量的数量积得出$\overrightarrow{a}$$•\overrightarrow{b}$=cos2A•$\frac{1}{co{s}^{2}A+1}$+sin2A•$\frac{1}{si{n}^{2}A-2}$=2+$\frac{3}{si{n}^{2}A-2}$,A∈(0,$\frac{π}{3}$],再利用单调性求解即可.
解答 解:∵A为△ABC的最小内角,若向量$\overrightarrow{a}$=(cos2A,sin2A),$\overrightarrow{b}$=($\frac{1}{co{s}^{2}A+1}$,$\frac{1}{si{n}^{2}A-2}$),
∴$\overrightarrow{a}$$•\overrightarrow{b}$=cos2A•$\frac{1}{co{s}^{2}A+1}$+sin2A•$\frac{1}{si{n}^{2}A-2}$=2+$\frac{3}{si{n}^{2}A-2}$,A∈(0,$\frac{π}{3}$]
根据函数解析式判断为减函数
∴最大值为:2-$\frac{3}{2}$=$\frac{1}{2}$,(此值取不着)
最小值为:2$+\frac{3}{\frac{3}{4}-2}$=$-\frac{2}{5}$
∴$\overrightarrow{a}$$•\overrightarrow{b}$的取值范围[$-\frac{2}{5}$,$\frac{1}{2}$)
故选:C
点评 本题考查了三角形的性质,平面向量的运算,性质,三角函数的单调性的运用,属于综合题目.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
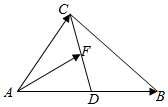 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )| A. | $6+2\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | $3+2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com