
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为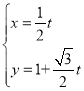 (t为参数),以直角坐标系
(t为参数),以直角坐标系![]() 的
的![]() 点为极点,
点为极点,![]() 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的倾斜角;
的倾斜角;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的长度.
的长度.
科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示在菱形ABCD中,![]() ,
,![]() ,点E是AD的中点,将
,点E是AD的中点,将![]() 沿BE折起,使得平面
沿BE折起,使得平面![]() 平面BCDE得到如图2所示的四棱锥
平面BCDE得到如图2所示的四棱锥![]() ,点F为AC的中点.在图2中
,点F为AC的中点.在图2中
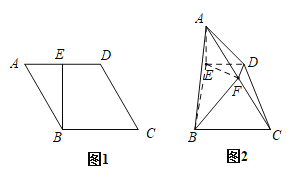
(Ⅰ)证明:![]() 平面ABE;
平面ABE;
(Ⅱ)求点A到平面BEF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关……”其大意为:“某人从距离关口三百七十八里处出发,第一天走得轻快有力,从第二天起,由于脚痛,每天走的路程为前一天的一半,共走了六天到达关口……” 那么该人第一天走的路程为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC的平面展开图中,四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:

(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且![]() ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性有10人.

(1)根据已知条件完成下面的![]() 列联表,并判断是否有90%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有90%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 10 | ||
总计 |
(2)将上述调査所得到的频率视为概率,现在从该地的网民中随机抽取3名,记被抽取的3名网民中的“网购达人”的人数为X,求X的分布列、数学期望![]() 和方差
和方差![]() .
.
参考公式: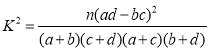 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() ,过其右焦点F的直线
,过其右焦点F的直线![]() 交椭圆C于M,N两点,交y轴于E点.若
交椭圆C于M,N两点,交y轴于E点.若![]() ,
,![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)试判断![]() 是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com