Question

5．如图，四棱锥S-ABCD的底面是正方形，SA⊥平面ABCD，SA=$\sqrt{2}$AB，点E在棱SC上．
（Ⅰ）若E为SC的中点，求证：SA∥平面BDE；
（Ⅱ）在（Ⅰ）的条件下，求CE与平面BDE所成的角．

Answer 1

分析 （Ⅰ）要证明SA∥平面BDE，只需证明SA平行于平面BDE内的一条直线即可，而E为中点，所以连接AC、BD交于点O．由条件知道O为AC中点，从而EO为三角形SAC的中位线，从而得到SA∥OE，得证；
（Ⅱ）证明∠CEO为CE与平面BDE所成的角，即可得出结论．

解答 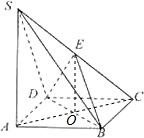（Ⅰ）证明：设AC与BD的交点为O，连接OE，
因为四边形ABCD是正方形，所以O为AC的中点，
又E为SC的中点，所以OE为三角形SAC的中位线，所以SA∥OE，
又OE?面BDE，SA?面BDE，
所以，SA∥平面BDE；
（Ⅱ）解：因为SA⊥平面ABCD，所以SA⊥OC，
因为SA∥EO，所以EO⊥OC，
因为四边形ABCD是正方形，所以BD⊥OC，
所以OC⊥平面BDE，
所以∠CEO为CE与平面BDE所成的角．
设正方形的边长为a，则EO=$\frac{1}{2}$SA=$\frac{\sqrt{2}}{2}$a，
Rt△COE中，tan∠CEO=$\frac{OC}{EO}$=1，所以∠CEO=45°，
所以CE与平面BDE所成的角为45°．

点评 本题考查线面平行的判定，直线与平面所成的觉，线面平行转化为线线平行是解题的关键．