练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．某学校需从3名男生和2名女生中选出4人，分派到甲、乙、丙三地参加义工活动，其中甲地需要选派2人且至少有1名女生，乙地和丙地各需要选派1人，则不同的选派方法的种数是（　　）
    A．18B．24C．36D．42

    分析 根据题意，先分析甲地的安排方法，分“分派2名女生”和“分派1名女生”两种情况讨论，由加法原理可得甲地的分派方法数目，第二步在剩余3人中，任选2人，安排在乙、丙两地，由排列数公式可得其安排方法数目，由分步计数原理计算可得答案．

    解答 解：根据题意，甲地需要选派2人且至少有1名女生，
    若甲地分派2名女生，有C22=1种情况，
    若甲地分配1名女生，有C21•C31=6种情况，
    则甲地的分派方法有1+6=7种，
    甲地安排好后，在剩余3人中，任选2人，安排在乙、丙两地，有A32=6种安排方法，
    则不同的选派方法的种数是7×6=42；
    故选：D．

    点评 本题考查排列、组合的实际应用，注意先分析受到限制的元素，如本题的甲地．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．已知双曲线过点（2，3），渐进线方程为y=±$\sqrt{3}$x，则双曲线的标准方程是（　　）
    A．$\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$B．$\frac{y^2}{3}-\frac{x^2}{2}=1$C．${x^2}-\frac{y^2}{3}=1$D．$\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知实数x，y满足$\left\{\begin{array}{l}x+2y-5≥0\\ x-3y+5≥0\\ kx-y-3k≤0\end{array}\right.$，若目标函数z1=3x+y的最小值的7倍与z2=x+7y的最大值相等，则实数k的值为（　　）
    A．1B．-1C．-2D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数$f（x）=2sin（{ωx+φ}）+1（{ω＞0，|φ|＜\frac{π}{2}}），f（α）=-1，f（β）=1$，若|α-β|的最小值为$\frac{3π}{4}$，且f（x）的图象关于点$（{\frac{π}{4}，1}）$对称，则函数f（x）的单调递增区间是（　　）
    A．$[{-\frac{π}{2}+2kπ，π+2kπ}]，k∈Z$B．$[{-\frac{π}{2}+3kπ，π+3kπ}]，k∈Z$
    C．$[{π+2kπ，\frac{5π}{2}+2kπ}]，k∈Z$D．$[{π+3kπ，\frac{5π}{2}+3kπ}]，k∈Z$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．某食品厂只做了3种与“福”字有关的精美卡片，分别是“富强福”、“和谐福”、“友善福”、每袋食品随机装入一张卡片，若只有集齐3种卡片才可获奖，则购买该食品4袋，获奖的概率为（　　）
    A．$\frac{3}{16}$B．$\frac{4}{9}$C．$\frac{3}{8}$D．$\frac{8}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．△ABC中，角A，B，C的对边分别为a，b，c，若a=$\frac{\sqrt{6}}{2}$b，A=2B，则cosB 等于（　　）
    A．$\frac{\sqrt{6}}{6}$B．$\frac{\sqrt{6}}{5}$C．$\frac{\sqrt{6}}{4}$D．$\frac{\sqrt{6}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

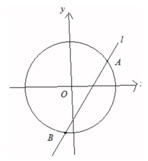    12．已知椭圆T：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，直线l经过点P（m，0）与T相交于A、B两点．
    （1）若C（0，-$\sqrt{3}$）且|PC|=2，求证：P必为Γ的焦点；
    （2）设m＞0，若点D在Γ上，且|PD|的最大值为3，求m的值；
    （3）设O为坐标原点，若m=$\sqrt{3}$，直线l的一个法向量为$\overrightarrow{n}$=（1，k），求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

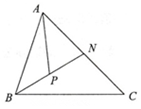
    9．如图，在△ABC中，N、P分别是AC、BN的中点，设$\overrightarrow{BA}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，则$\overrightarrow{AP}$=（　　）
    A．$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$B．-$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$C．-$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$D．$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知函数f（x）=sin（ωx+φ）（ω＞，|φ|＜$\frac{π}{2}$），其图象相邻两个对称中心的距离为$\frac{π}{2}$，且f（x+$\frac{π}{6}$）=f（-x），下列判断正确的是　（　　）
    A．函数f（x）的最小正周期为2π
    B．函数f（x）的图象关于点（$\frac{7π}{12}$，0）对称
    C．函数f（x）在[$\frac{3π}{4}$，π]上单调递增
    D．函数f（x）的图象关于直线x=-$\frac{7π}{12}$对称

    查看答案和解析>>

    同步练习册答案