Question

19．在四棱锥P-ABCD中，PA⊥面ABCD，∠DAB=90°，AB平行于CD，AD=CD=2AB=2，E，F分别为PC，CD的中点
（1）求证：AB⊥面BEF；
（2）设PA=h，若二面角E-BD-C大于45°，求h的取值范围．

Answer 1

分析 （1）以AB所在直线为x轴，以AD所在直线为y轴，以AP所在直线为z轴建立空间直角坐标系，利用向量法能证明AB⊥面BEF．
（2）求出面BCD的法向量和面DE的法向量，利用向量法能求出h的取值范围．

解答 证明：（1）以AB所在直线为x轴，以AD所在直线为y轴，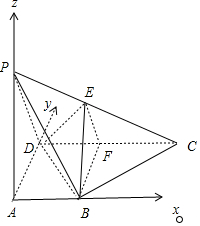
以AP所在直线为z轴建立空间直角坐标系，
则A（0，0，0），P（0，0，h），B（1，0，0），D（0，2，0），C（2，2，0），

E（1，1，$\frac{h}{2}$），F（1，2，0），
$\overrightarrow{BE}$=（0，1，$\frac{h}{2}$），$\overrightarrow{BF}$=（0，2，0），$\overrightarrow{CD}$=（-2，0，0），
∴$\overrightarrow{BE}•\overrightarrow{CD}$=0，$\overrightarrow{BF}•\overrightarrow{CD}$=0，
∴CD⊥BE，CD⊥BF，∴CD⊥面BEF．
∵AB平行于CD，∴AB⊥面BEF．

解：（2）设面BCD的法向量为$\overrightarrow{n}$，则$\overrightarrow{n}$（0，0，1），
设面BDE的法向量为$\overrightarrow{m}$（x，y，z），
∵$\overrightarrow{BD}$=（-1，2，0），$\overrightarrow{BE}$=（0，1，$\frac{h}{2}$），
∴$\left\{\begin{array}{l}{\overrightarrow{BD}•\overrightarrow{m}=-x+2y=0}\\{\overrightarrow{BE}•\overrightarrow{m}=y+\frac{h}{2}z=0}\end{array}\right.$，取x=2，得$\overrightarrow{m}$=（2，1，-$\frac{2}{h}$），
∵二面角E-BD-C大于45°，
∴cos＜$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$＞=$\frac{\frac{2}{h}}{\sqrt{5+\frac{4}{{h}^{2}}}}$＜cos45°=$\frac{\sqrt{2}}{2}$，
由h＞0，解得h＞$\frac{2\sqrt{5}}{5}$，
∴h的取值范围是（$\frac{2\sqrt{5}}{5}$，+∞）．

点评 本题考查线面垂直的证明，考查实数的取值范围的求法同，是中档题，解题时要认真审题，注意向量法的合理运用．