
分析 先设切点,然后利用切点来寻找切线斜率的联系,以及对应的函数值,综合联立求解即可
解答 解:设y=kx+b与y=lnx+2和y=ln(x+1)的切点分别为(x1,kx1+b)、(x2,kx2+b);
由导数的几何意义可得k=$\frac{1}{{x}_{1}}$=$\frac{1}{{x}_{2}+1}$,得x1=x2+1
再由切点也在各自的曲线上,可得$\left\{\begin{array}{l}{k{x}_{1}+b=ln{x}_{1}+2}\\{k{x}_{2}+b=ln{(x}_{2}+1)}\end{array}\right.$
联立上述式子解得$\left\{\begin{array}{l}{k=2}\\{{x}_{1}=\frac{1}{2}}\\{{x}_{2}=-\frac{1}{2}}\end{array}\right.$;
从而kx1+b=lnx1+2得出b=1-ln2.
点评 本题考查了导数的几何意义,体现了方程思想,对学生综合计算能力有一定要求,中档题


科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 14 | C. | 13 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
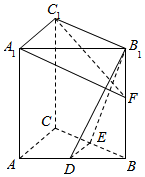 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com