
分析 (1)易知x=0是y=f(x)的零点,从而x>0时,f(x)=x(x2-1-$\frac{1}{\sqrt{x}}$),设φ(x)=x2-1-$\frac{1}{\sqrt{x}}$,利用导数及零点判定定理可求函数零点个数;
(2)化简得g(x),其定义域是(0,1)∪(1,+∞),求导得g'(x),构造h(x)=x2-(2+a)x+1,则问题转化为h(x)=0有两个不同的根x1,x2,从而△>0,且一根在(0,$\frac{1}{e}$)内,不妨设0<x1<$\frac{1}{e}$,再由x1x2=1,得0<x1<$\frac{1}{e}$<e<x2,根据零点判定定理可知只需h($\frac{1}{e}$)<0,由此可求a的范围;
(3)可求y=g(x)在(1,+∞)内的最小值为g(x2),y=g(x)在(0,1)内的最大值为g(x1),可知x1+x2=2+a,x1x2=1,x1∈(0,$\frac{1}{e}$),x2∈(e,+∞),故g(t)-g(s)≥g(x2)-g(x1)═lnx22+x2-$\frac{1}{{x}_{2}}$(x2>e),设k(x)=lnx2+x-$\frac{1}{x}$=2lnx+x-$\frac{1}{x}$,k'(x)=$\frac{2}{x}$+1+$\frac{1}{{x}^{2}}$>0,利用导数可判断k(x)在(e,+∞)内单调递增,从而有k(x)>k(e),整理可得结论.
解答 解:(1)∵f(0)=0,∴x=0是y=f(x)的一个零点,
当x>0时,f(x)=x(x2-1-$\frac{1}{\sqrt{x}}$),设φ(x)=x2-1-$\frac{1}{\sqrt{x}}$,
φ'(x)=2x+$\frac{1}{2\sqrt{{x}^{3}}}$>0,∴φ(x)在(0,+∞)上单调递增.
又φ(1)=-1<0,φ(2)=3-$\frac{1}{\sqrt{2}}$>0,
故φ(x)在(1,2)内有唯一零点,
因此y=f(x)在(0,+∞)内有且仅有2个零点;
(2)g(x)=$\frac{a{x}^{2}+ax}{f(x)+\sqrt{x}}$+lnx=lnx+$\frac{a}{x-1}$,
其定义域是(0,1)∪(1,+∞),
则g'(x)=$\frac{1}{x}$-$\frac{a}{{(x-1)}^{2}}$=$\frac{{x}^{2}-(2+a)x+1}{{x(x-1)}^{2}}$,
设h(x)=x2-(2+a)x+1,要使函数y=g(x)在(0,$\frac{1}{e}$)内有极值,则h(x)=0有两个不同的根x1,x2,
∴△=(2+a)2-4>0,得a>0或a<-4,且一根在(0,$\frac{1}{e}$)内,不妨设0<x1<$\frac{1}{e}$,
又x1x2=1,∴0<x1<$\frac{1}{e}$<e<x2,
由于h(0)=1,则只需h($\frac{1}{e}$)<0,即$\frac{1}{{e}^{2}}$-(a+2)•$\frac{1}{e}$+1<0,
解得a>e+$\frac{1}{e}$-2;
(3)由(2)可知,当x∈(1,x2)时,g'(x)<0,g(x)递减,x∈(x2,+∞)时,g'(x)>0,g(x)递增,
故y=g(x)在(1,+∞)内的最小值为g(x2),即t∈(1,+∞)时,g(t)≥g(x2),
又当x∈(0,x1)时,g'(x)>0,g(x)单调递增,x∈(x1,1)时,g'(x)<0,g(x)单调递减,
故y=g(x)在(0,1)内的最大值为g(x1),即对任意s∈(0,1),g(s)≤g(x1),
由(2)可知x1+x2=2+a,x1x2=1,x1∈(0,$\frac{1}{e}$),x2∈(e,+∞),
因此,g(t)-g(s)≥g(x2)-g(x1)=lnx2+$\frac{a}{{x}_{2}-1}$-lnx1-$\frac{a}{{x}_{1}-1}$=ln $\frac{{x}_{2}}{{x}_{1}}$+$\frac{a}{{x}_{2}-1}$-$\frac{a}{{x}_{1}-1}$=lnx22+x2-$\frac{1}{{x}_{2}}$(x2>e),
设k(x)=lnx2+x-$\frac{1}{x}$=2lnx+x-$\frac{1}{x}$,k'(x)=$\frac{2}{x}$+1+$\frac{1}{{x}^{2}}$>0,
∴k(x)在(e,+∞)内单调递增,
故k(x)>k(e)=2+e-$\frac{1}{e}$,即g(t)-g(s)>e+2-$\frac{1}{e}$.
点评 本题考查利用导数研究函数的零点、极值、最值,考查转化思想,考查学生综合运用数学知识分析解决问题的能力,综合性强,能力要求比较高.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
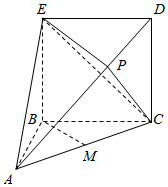 在几何体ABCDE中,矩形BCDE的边CD=2,BC=AB=1,∠ABC=90°,直线EB⊥平面ABC,P是线段AD上的点,且AP=2PD,M为线段AC的中点.
在几何体ABCDE中,矩形BCDE的边CD=2,BC=AB=1,∠ABC=90°,直线EB⊥平面ABC,P是线段AD上的点,且AP=2PD,M为线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,AB=4,BC=2$\sqrt{3}$,四边形CDEF是菱形,∠DEF=60°,且平面CDEF⊥平面ABCD,M,N分别是线段EF,CD上的点,满足EM=3MF.CN=3ND,AC与BN交于点P.
如图,四边形ABCD是矩形,AB=4,BC=2$\sqrt{3}$,四边形CDEF是菱形,∠DEF=60°,且平面CDEF⊥平面ABCD,M,N分别是线段EF,CD上的点,满足EM=3MF.CN=3ND,AC与BN交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
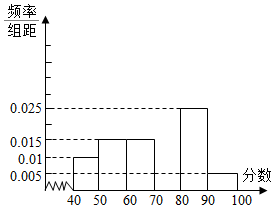 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{4}^{3}$0.83×0.2 | B. | C${\;}_{4}^{3}$0.83 | C. | 0.83×0.2 | D. | C${\;}_{4}^{3}$0.8×0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com