Question

10．已知函数f（x）=（x-t）|x|（t∈R）．
（Ⅰ）当t=2时，求函数f（x）的单调性；
（Ⅱ）试讨论函数f（x）的单调区间；
（Ⅲ）若?t∈（0，2），对于?x∈[-1，2]，不等式f（x）＞x+a都成立，求实数a的取值范围．

Answer 1

分析 （Ⅰ）当t=2时，f（x）=（x-t）|x|=$\left\{\begin{array}{l}{{x}^{2}-2x，}&{（x≥0）}\\{{-x}^{2}+2x，}&{（x＜0）}\end{array}\right.$，作出其图象，利用二次函数的单调性可求函数f（x）的单调性；
（Ⅱ）分t＞0、t=0、t＜0三类讨论，可求得函数f（x）的单调区间；
（Ⅲ）设g（x）=f（x）-x=$\left\{\begin{array}{l}{{x}^{2}-（t+1）x，x∈[0，2]}\\{{-x}^{2}+（t-1）x，x∈[-1，0]}\end{array}\right.$，依题意，可求得g_min（x）=-t，只须?t∈（0，2），使得：$\left\{\begin{array}{l}{-\frac{{（t+1）}^{2}}{4}＞a}\\{-t＞a}\end{array}\right.$成立，解之即可求得实数a的取值范围．

解答 解：（Ⅰ）当t=2时，f（x）=（x-t）|x|=$\left\{\begin{array}{l}{{x}^{2}-2x，}&{（x≥0）}\\{{-x}^{2}+2x，}&{（x＜0）}\end{array}\right.$，
根据二次函数的图象与性质可得：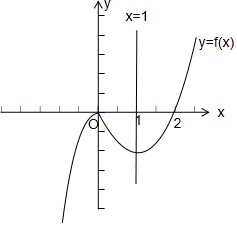

f（x）在（-∞，0）上单调递增，（0，1）上单调递减，（1，+∞）上单调递增．…（3分）
（Ⅱ）f（x）=$\left\{\begin{array}{l}{{x}^{2}-tx，}&{（x≥0）}\\{{-x}^{2}+tx，}&{（x＜0）}\end{array}\right.$，…（4分）
当t＞0时，f（x）的单调增区间为[$\frac{t}{2}$，+∞），（-∞，0]，单调减区间为[0，$\frac{t}{2}$]，…（6分）
当t=0时，f（x）的单调增区间为R…（8分）
当t＜0时，f（x）的单调增区间为[0，+∞），（-∞，$\frac{t}{2}$]，单调减区间为[$\frac{t}{2}$）…（10分）
（Ⅲ）设g（x）=f（x）-x=$\left\{\begin{array}{l}{{x}^{2}-（t+1）x，x∈[0，2]}\\{{-x}^{2}+（t-1）x，x∈[-1，0]}\end{array}\right.$，
x∈[0，2]时，∵$\frac{t+1}{2}$∈（0，2），∴g_min（x）=g（$\frac{t+1}{2}$）=-$\frac{{（t+1）}^{2}}{4}$…（11分）
x∈[-1，0]时，∵g（-1）=-t，g（0）=0，∴g_min（x）=-t…（12分）
故只须?t∈（0，2），使得：$\left\{\begin{array}{l}{-\frac{{（t+1）}^{2}}{4}＞a}\\{-t＞a}\end{array}\right.$成立，即$\left\{\begin{array}{l}{-\frac{1}{4}≥a}\\{0≥a}\end{array}\right.$．…（14分）
所以a≤-$\frac{1}{4}$…（15分）

点评 本题考查函数恒成立问题，突出考查二次函数的单调性与最值，考查数形结合思想与函数与方程思想的综合运用，属于难题．