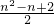Question

己知数列{a_n}，{b_n}，{c_n}的通项满足b_n=a_n+1-a_n，c_n=b_n+1-b_n（n∈N?），若{b_n}是一个非零常数列，则称数列{a_n}是一阶等差数列；若{c_n}是一个非零常数列，则称数列{a_n}是二阶等差数列，写出满足条件a₁=1，b₁=1，c_n=1的二阶等差数列．{a_n}的第5项即a₅=________；数列{a_n}的通项公式a_n=________．

Answer 1

11    
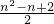
分析：根据a₁=1，b₁=1，c_n=1的二阶等差数列，推出{b_n}的通项公式，b_n=n，然后确定a_n，求出a₅的值；推出通项公式a_n．
解答：因为a₁=1，b₁=1，c_n=1的二阶等差数列．c_n=b_n+1-b_n（n∈N?），所以b_n=n，则a_n+1-a_n=n，
所以a₅=4+a₄=4+3+a₃=4+3+2+a₂=4+3+2+1+a₁=11；
因为a_n+1-a_n=n
所以a₂-a₁=1
a₃-a₂=2
a₄-a₃=3
…
a_n-a_n-1=n-1
所以a_n-a₁=1+2+3+4+…+（n-1）==
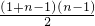
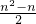
所以a_n=．
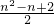
故答案为：11；
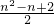
点评：本题是中档题，考查数列通项公式的求法，新定义的应用，考查发现问题解决问题的能力，考查学生的细心程度与心态．
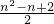
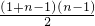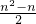
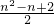