
分析 先设生产甲、乙两种产品分别为x千克,y千克,其利产值为z元,列出约束条件,再根据约束条件画出可行域,设z=600x+400y,再利用z的几何意义求最值,只需求出直线z=600x+400y过可行域内的点时,从而得到z值即可.
解答 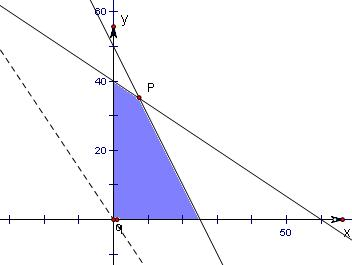 解析:设生产甲、乙两种产品分别为x千克,y千克,其利产值为z元,
解析:设生产甲、乙两种产品分别为x千克,y千克,其利产值为z元,
根据题意,可得约束条件为$\left\{\begin{array}{l}{4x+2y≤100}\\{2x+3y≤120}\\{x≥0,y≥0}\end{array}\right.$…(3分)
作出可行域如图:….(5分)
目标函数z=600x+400y,
作直线l0:3x+2y=0,再作一组平行于l0的直线l:3x+2y=z,当直线l经过P点时z=600x+400y取得最大值,….(9分)
由 $\left\{\begin{array}{l}{4x+2y=100}\\{2x+3y=120}\end{array}\right.$,
解得交点P( 7.5,35)….(12分)
所以有z最大=600×7.5+400×35=18500(元)…(13分)
所以生产甲产品7.5千克,乙产品35千克时,总产值最大,为18500元.…(14分).
故答案为:7.5;35.
点评 本题是一道方案设计题型,考查了列一元一次不等式组解实际问题的运用及一元一次不等式组的解法的运用,解答时找到题意中的不相等关系是建立不等式组的关键.


科目:高中数学 来源: 题型:选择题
| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17π}{6}$ | B. | $\frac{17π}{3}$ | C. | 5π | D. | $\frac{13π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
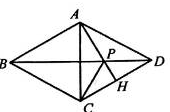 如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC
如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com