
分析 根据分段函数的表达式进行求解即可a的值,讨论x的取值范围结合指数不等式和对数不等式的解法进行求解即可.
解答 解:∵当a-3≤0时,f(x)=($\frac{1}{2}$)a-3-1=0,此时方程无解,
∴a-3≤0不成立,
当a-3>0时,即a>3,
则由f(a-3)=0得log${\;}_{\frac{1}{3}}$(a-3)=0,则a-3=1,得a=4,
最大不等式f(x)>a等价为f(x)>4,
若x≤0时,f(x)=($\frac{1}{2}$)x-1>4,得x-1<-2.得x<-1,
当x>0时,f(x)>4,得log${\;}_{\frac{1}{3}}$x>4得0<x<$\frac{1}{81}$,
综上不等式的解集为{x|x<-1或0<x<$\frac{1}{81}$},
故答案为:4,{x|x<-1或0<x<$\frac{1}{81}$}
点评 本题主要考查分段函数的应用,根据分段函数的表达式进行讨论求解是解决本题的关键.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
| 不及格 | 及格 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
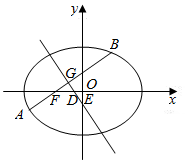 椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左焦点为F,右顶点为A1,过点F斜率为k的直线交椭圆C于A,B两点,线段AB的中点为G,线段AB的垂直平分线交x轴于点D,交y轴于点E,O是坐标原点,记△GFD的面积为S1,记△OED的面积为S2
椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左焦点为F,右顶点为A1,过点F斜率为k的直线交椭圆C于A,B两点,线段AB的中点为G,线段AB的垂直平分线交x轴于点D,交y轴于点E,O是坐标原点,记△GFD的面积为S1,记△OED的面积为S2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
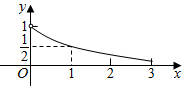 已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )
已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )| A. | 2x | B. | $-{(\frac{1}{2})^x}$ | C. | ${({\frac{1}{2}})^x}$ | D. | -2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com