

���� �������ۣ����շ���һ������Ҫ��������ۣ�
����һ����OC����$��POC=x��x�ʣ�0��\frac{��}{4}��$�������ABCD�����Ϊy����y=AB•BC��ͨ�����뻯�������Ǻ�������ֵȷ�������������Եó��𰸣�
������������POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE����$��MOE=�������ʣ�0��\frac{��}{6}��$�������EFGH�����ΪS�����S��ʽ�ӣ������Ǻ��������������ֵ��
��Ƚ϶������ֵ�Ĵ�С��ѡ�����ֵ���ɵó��𰸣�
��� �⣺������һ����ͼ����OC����$��POC=x��x�ʣ�0��\frac{��}{4}��$��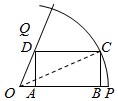
��Rt��OBC��BC=Rsinx��OB=Rcosx����DA=Rsinx
��Rt��OAD��$\frac{DA}{OA}=tan\frac{��}{3}$����$OA=\frac{{\sqrt{3}}}{3}DA=\frac{{\sqrt{3}}}{3}Rsinx$��
��$AB=OB-OA=R��cosx-\frac{{\sqrt{3}}}{3}sinx��$�������ABCD�����Ϊy����
y=AB•BC=${R}^{2}��sinxcosx-\frac{\sqrt{3}}{3}si{n}^{2}x��$=$\frac{\sqrt{3}}{3}$sin��2x+$\frac{��}{6}$��-$\frac{\sqrt{3}}{6}$��
��$x�ʣ�0��\frac{��}{3}��$��$\frac{��}{6}��2x+\frac{��}{6}��\frac{5��}{6}$��
���Ե�$2x+\frac{��}{6}=\frac{��}{2}$����$x=\frac{��}{6}$ʱ${y_{max}}=��\frac{{\sqrt{3}}}{3}-\frac{{\sqrt{3}}}{6}��{R^2}=\frac{{\sqrt{3}}}{6}{R^2}$��
������������ͼ����POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE��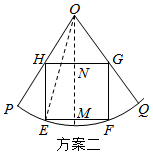
��$��MOE=�������ʣ�0��\frac{��}{6}��$����Rt��MOE�У�ME=Rsin����OM=Rcos��
��Rt��ONH��$\frac{NH}{ON}=tan\frac{��}{6}$����$ON=\sqrt{3}NH=\sqrt{3}Rsin��$��
��$MN=OM-ON=R��cos��-\sqrt{3}sin����$�������EFGH�����ΪS��
��S=2ME•MN=2R2sin����cos��-$\sqrt{3}$sin����=R2��sin2��+$\sqrt{3}$cos2��-$\sqrt{3}$��=$2{R^2}sin��2��+\frac{��}{3}��-\sqrt{3}{R^2}$
��$���ʣ�0��\frac{��}{6}��$����$\frac{��}{3}��2��+\frac{��}{3}��\frac{2��}{3}$�����Ե�$2��+\frac{��}{3}=\frac{��}{2}$����$��=\frac{��}{12}$ʱ${S_{max}}=��2-\sqrt{3}��{R^2}$��$\frac{{\sqrt{3}}}{6}-2+\sqrt{3}=\frac{{7\sqrt{3}-12}}{6}��0$����ymax��Smax
�𣺸�������������߽��飺ѡ�÷���һ���ã�
���� ���⿼��ѧ���ļ�������������ѧ����ת���������Լ���������֪ʶ�������ʵ������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 6 | C�� | 2��1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | 6 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
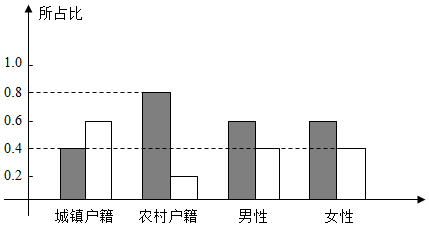
| A�� | �Ƿ�����ѡ��������̥�뻧���� | |
| B�� | �Ƿ�����ѡ��������̥���Ա��� | |
| C�� | ����ѡ��������̥����Ա�У�����������Ů��������ͬ | |
| D�� | ����ѡ��������̥����Ա�У�ũ�廧���������ڳ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
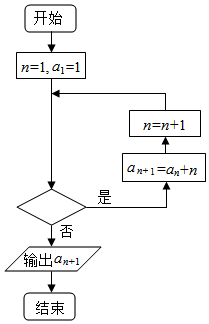 ��֪����{an}�У�a1=-1��an+1=an+n����������ͼ��ʾ�ij����ͼ��������еĵ�2016����жϿ��ڵ������ǣ�������
��֪����{an}�У�a1=-1��an+1=an+n����������ͼ��ʾ�ij����ͼ��������еĵ�2016����жϿ��ڵ������ǣ�������| A�� | n��2014�� | B�� | n��2015�� | C�� | n��2016�� | D�� | n��2017�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com