
| A�� | �Ƿ�����ѡ��������̥�뻧���� | |
| B�� | �Ƿ�����ѡ��������̥���Ա��� | |
| C�� | ����ѡ��������̥����Ա�У�����������Ů��������ͬ | |
| D�� | ����ѡ��������̥����Ա�У�ũ�廧���������ڳ������� |
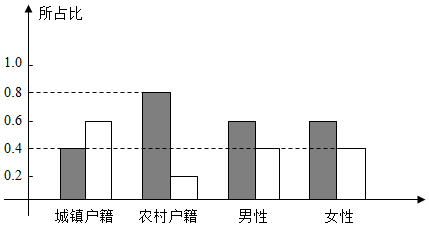
���� �ɱ���ͼ���ɵ��Ƿ�����ѡ��������̥�뻧�����Ա��йأ�����ѡ��������̥����Ա�У�ũ�廧���������ڳ�������������ѡ��������̥����Ա�е�����������Ů�����������ɵó����ۣ�
��� �⣺�ɱ���ͼ���ɵ��Ƿ�����ѡ��������̥�뻧�����Ա��йأ�
����ѡ��������̥����Ա�У�ũ�廧���������ڳ���������
����ѡ��������̥����Ա�У���������Ϊ0.6��60=36��Ů������0.4��60=24������ͬ��
��ѡ��D
���� ���⿼�����ͼ������ѧ����������������������ȷ�������ͼ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
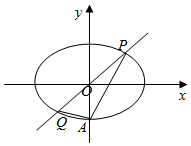 ��ͼ����ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������A��0��-1������������Ϊ$\frac{\sqrt{2}}{2}$��
��ͼ����ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������A��0��-1������������Ϊ$\frac{\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com