
分析 (1)由已知得a2,a3是方程x2-14x+45=0的两根,且a2<a3,从而得到a2=5,a3=9,由此能求出an.
(2)先求出Sn=n(2n-1),bn=$\frac{S_n}{n+c}$=$\frac{n(2n-1)}{n+c}$,c≠0,由此能证明当且仅当c=-$\frac{1}{2}$时,数列{bn}为等差数列.
(3)Cn=$\frac{8}{(4n+4)•2n}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,从而得到f(n)=4(n-1)•0.9n,(n∈N*),由此能求出存在整数M,使f(n)<M对一切n∈N*都成立,并能求出M的最小值.
解答 解:(1)∵等差数列an中,公差d>0,满足a2•a3=45,a1+a4=14.
∴a2•a3=45,a1+a4=a2+a3=14.
∴a2,a3是方程x2-14x+45=0的两根,且a2<a3,
解方程x2-14x+45=0,得a2=5,a3=9,
∴d=a3-a2=9-5=4,a1=a2-4=1,
∴an=1+(n-1)×4=4n-3.
证明:(2)Sn=n×$1+\frac{n(n-1)}{2}×4$=n(2n-1),
bn=$\frac{S_n}{n+c}$=$\frac{n(2n-1)}{n+c}$,c≠0,
由2b2=b1+b3,得$\frac{12}{2+c}$=$\frac{1}{1+c}+\frac{15}{3+c}$,
化简得2c2+c=0,c≠0,∴c=-$\frac{1}{2}$.
反之,令c=-$\frac{1}{2}$,即得bn=2n,数列bn为等差数列,
∴当且仅当c=-$\frac{1}{2}$时,数列{bn}为等差数列.
(3)∵cn=$\frac{8}{{({a_n}+7)•{b_n}}}$(n∈N*),
∴Cn=$\frac{8}{(4n+4)•2n}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴数列{cn}的前n项和为Tn=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
∵f(n)=Tn•(an+3-$\frac{8}{{b}_{n}}$)•0.9n(n∈N*),
∴f(n)=$\frac{n}{n+1}$(4n-3+3-$\frac{8}{2n}$)•0.9n=$\frac{n}{n+1}$(4n-$\frac{4}{n}$)•0.9n=4(n-1)•0.9n,(n∈N*),
f(1)=0,f(2)=4×0.92=3.24,f(3)=8×0.93=5.832,
f(n+1)-f(n)=4n•0.9n+1-4(n-1)•0.9n=4×0.9n-0.4n×0.9n=0.9n(4-0.4n),
由f(n+1)-f(n)=0.9n(4-0.4n)≥0,得n≤10,
∴存在整数M,使f(n)<M对一切n∈N*都成立,
M的最小值为f(10)=4(10-1)×0.910=36×0.910.
点评 本题考查数列的通项公式的求法,考查等差数列的证明,考查满足条件的最小值的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
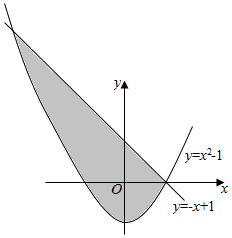 计算下列定积分:
计算下列定积分:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
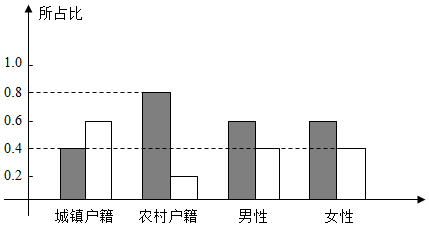
| A. | 是否倾向选择生育二胎与户籍无关 | |
| B. | 是否倾向选择生育二胎与性别无关 | |
| C. | 倾向选择生育二胎的人员中,男性人数与女性人数相同 | |
| D. | 倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
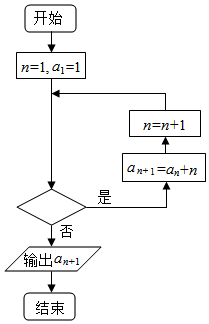 已知数列{an}中,a1=-1,an+1=an+n,若利用如图所示的程序框图计算该数列的第2016项,则判断框内的条件是( )
已知数列{an}中,a1=-1,an+1=an+n,若利用如图所示的程序框图计算该数列的第2016项,则判断框内的条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n≤2016? | D. | n≤2017? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{4}$ | B. | 5 | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com