
分析 根据向量数量积的关系进行化简,结合向量投影的定义进行求解即可.
解答 解:∵$\overrightarrow{a}$与$\overrightarrow b$的夹角为120°,若$(\overrightarrow a+\overrightarrow b)⊥(\overrightarrow a-\overrightarrow b)$,且$|\overrightarrow a|=2$,
∴($\overrightarrow{a}$+$\overrightarrow b$)•($\overrightarrow{a}$-$\overrightarrow b$)=0,即$\overrightarrow{a}$2=$\overrightarrow b$2,则|$\overrightarrow{a}$|=|$\overrightarrow b$|=2,
则$\overrightarrow{a}$•$\overrightarrow b$=|$\overrightarrow{a}$||$\overrightarrow b$|cos120°=$-\frac{1}{2}×2×2$=-2,
则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的正射影为$\frac{\overrightarrow{b}•\overrightarrow{a}}{|\overrightarrow{a}|}$=$\frac{-2}{2}=-1$,
故答案为:-1
点评 本题主要考查向量数量积的应用,根据向量垂直求出$\overrightarrow{a}$•$\overrightarrow b$以及利用向量射影的定义是解决本题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
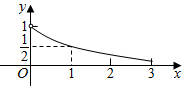 已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )
已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )| A. | 2x | B. | $-{(\frac{1}{2})^x}$ | C. | ${({\frac{1}{2}})^x}$ | D. | -2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com