
 是方程
是方程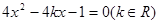 的两个不等实根,函数
的两个不等实根,函数 的定义域为
的定义域为 .
. 时,求函数
时,求函数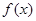 的值域;
的值域;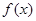 在其定义域
在其定义域 上是增函数;
上是增函数; ,
, 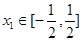 ,总存在
,总存在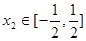 ,使得
,使得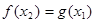 成立,
成立, 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:填空题
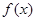 =
=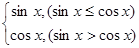 ,给出下列四个命题:①该函数是以
,给出下列四个命题:①该函数是以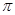 为最小正周期的周期函数;②当且仅当
为最小正周期的周期函数;②当且仅当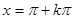 (k∈Z)时,该函数取得最小值-1;
(k∈Z)时,该函数取得最小值-1;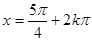 (k∈Z)对称;
(k∈Z)对称;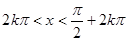 (k∈Z)时,0<
(k∈Z)时,0<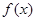 ≤
≤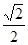 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
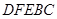 内修建一个矩形
内修建一个矩形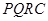 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且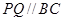 ,
,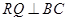 ,另外
,另外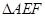 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量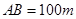 ,
,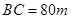 ,
, 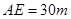 ,
,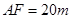 .
.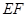 的方程;
的方程;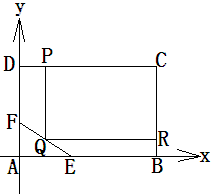
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com