
【题目】△ABC的内角A,B,C的对边分别为a,b,c,且(![]() b+c)tanC=﹣ctanA.
b+c)tanC=﹣ctanA.
(1)求A;
(2)若b![]() ,c=2,点D在BC边上,且AD=BD,求AD的长.
,c=2,点D在BC边上,且AD=BD,求AD的长.
【答案】(1)A![]() ;(2)AD
;(2)AD![]()
【解析】
(1)在(![]() b+c)tanC=﹣ctanA中利用同角公式切化弦和正弦定理边化角可得答案;
b+c)tanC=﹣ctanA中利用同角公式切化弦和正弦定理边化角可得答案;
(2)先用余弦定理求得![]() ,然后求得
,然后求得![]() ,再在△
,再在△![]() 中用余弦定理求得
中用余弦定理求得![]() 即可.
即可.
(1)∵(![]() b+c)tanC=﹣ctanA,∴(
b+c)tanC=﹣ctanA,∴(![]() )
)![]() c
c![]() ,
,
利用正弦定理边化角得:(![]() sinB+sinC)
sinB+sinC)![]() sinC
sinC![]() ,∵0<C<π,∴sinC≠0,
,∵0<C<π,∴sinC≠0,
∴(![]() sinB+sinC)
sinB+sinC)![]() ,∴
,∴![]() sinBcosA+sinCcosA=﹣sinAcosC,
sinBcosA+sinCcosA=﹣sinAcosC,
∴![]() sinBcosA=﹣(sinAcosC+sinCcosA)=﹣sin(A+C)=﹣sinB,
sinBcosA=﹣(sinAcosC+sinCcosA)=﹣sin(A+C)=﹣sinB,
又∵0<B<π,∴sinB≠0,∴![]() cosA=﹣1,∴cosA
cosA=﹣1,∴cosA![]() ,又∵0<A<π,∴A
,又∵0<A<π,∴A![]() ;
;
(2)∵A![]() ,b
,b![]() ,c=2,∴由余弦定理得:cosA
,c=2,∴由余弦定理得:cosA![]() ,
,
∴![]() ,∴a
,∴a![]() ,∴cosB
,∴cosB![]() ,
,
∴在三角形ABD中,由余弦定理得:cosB![]() ,且BD=AD,
,且BD=AD,
![]()
![]() ,∴AD
,∴AD![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
①每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
②每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③每位参加者按问题A、B、C、D顺序作答,直至答题结束.
假设甲同学对问题A、B、C、D回答正确的概率依次为![]() 、
、![]() 、
、![]() 、
、![]() ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(1)求甲同学能进入下一轮的概率;
(2)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x![]() a在(1,+∞)上有实根;命题q:方程
a在(1,+∞)上有实根;命题q:方程![]() 1表示的曲线是焦点在x轴上的椭圆.
1表示的曲线是焦点在x轴上的椭圆.
(1)若p是真命题,求a的取值范围;
(2)若p∧q是真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,
,![]() .有下列命题:
.有下列命题:
①对![]() ,恒有
,恒有![]() 成立.
成立.
②![]() ,使得
,使得![]() 成立.
成立.
③“若![]() ,则有
,则有![]() 且
且![]() .”的否命题.
.”的否命题.
④“若![]() 且
且![]() ,则有
,则有![]() .”的逆否命题.
.”的逆否命题.
其中,真命题有_____________.(只需填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
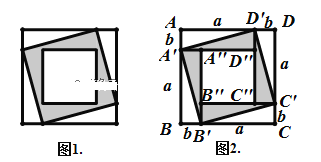
【题目】下图1,是某设计员为一种商品设计的平面logo样式.主体是由内而外的三个正方形构成.该图的设计构思如图2,中间正方形![]() 的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为
的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为![]() ,最内正方形
,最内正方形![]() 的面积为
的面积为![]() .当
.当![]() ,且
,且![]() 取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差
的公差![]() ,数列
,数列![]() 满足
满足![]() ,集合
,集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() ,求
,求![]() 使得集合
使得集合![]() 恰好有两个元素;
恰好有两个元素;
(3)若集合![]() 恰好有三个元素:
恰好有三个元素:![]() ,
,![]() 是不超过7的正整数,求
是不超过7的正整数,求![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com