秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法。如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例，若输入n，x的值分别为3，2，则输出v的值为
（A）35 （B）20 （C）18 （D）9
英才计划期末调研系列答案
精英口算卡系列答案科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（山东卷参考版） 题型：填空题
已知函数
其中
，若存在实数b，使得关于x的方程f（x）=b有三个不同的根，则m的取值范围是________________．
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（四川卷参考版） 题型：解答题
我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准
（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9组，制成了如图所示的频率分布直方图.
（Ⅰ）求直方图中a的值；
（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；
（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（四川卷参考版） 题型：解答题
已知椭圆E：
（a﹥b﹥0）的一个焦点与短轴的两个端点是正三角形的三个顶点，点P（
，
）在椭圆E上。
（Ⅰ）求椭圆E的方程；
（Ⅱ）设不过原点O且斜率为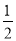
的直线l与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D，证明：︳MA︳·︳MB︳=︳MC︳·︳MD︳
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（四川卷参考版） 题型：选择题
抛物线y2=4x的焦点坐标是
（A）（0,2） （B）（0,1） （C）（2,0） （D）（1,0）
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试理科数学（浙江卷参考版） 题型：解答题
在△ABC中，内角A，B，C所对的边分别为a，b，c. 已知b+c=2a cos B.
（Ⅰ）证明：A=2B；
（Ⅱ）若△ABC的面积
，求角A的大小.
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（浙江卷参考版） 题型：解答题
如图，设抛物线
的焦点为F，抛物线上的点A到y轴的距离等于|AF|-1．
（Ⅰ）求p的值；
（Ⅱ）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x轴交于点M．求M的横坐标的取值范围．
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试数学（江苏卷参考版） 题型：填空题
已知一组数据4.7,4.8,5.1,5.4,5.5，则该组数据的方差是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
为整数的概率= 。