
| A. | $-\frac{3}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |
分析 可先画出图形,并连接AC,这样在△ABC中,根据AB=BC=1,∠BAC=30°即可求出AC的长度,从而便可求出$\overrightarrow{AB}•\overrightarrow{AC}$的值.
解答 解:如图,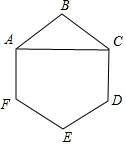
在△ABC中,AB=BC=1,∠BAC=30°;
∴$AC=2cos30°=\sqrt{3}$;
∴$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cos30°$=$1×\sqrt{3}×\frac{\sqrt{3}}{2}=\frac{3}{2}$.
故选D.
点评 考查三角函数的定义,清楚正六边形的内角为120°,以及向量数量积的计算公式.


科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 45°或135° | C. | 30° | D. | 30°或150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{7}$ | B. | $\sqrt{31}$ | C. | $\sqrt{34}$ | D. | $\sqrt{37}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
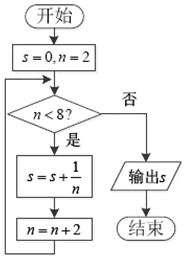
| A. | $\frac{3}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {1,2,3,4,5,6,8,10} | ||
| C. | {1,2,3,4,5} | D. | {2,4,6,8,10} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com