
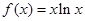 ,
,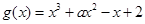 ,
,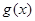 的两个极值点为
的两个极值点为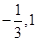 ,求函数
,求函数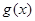 的解析式;
的解析式;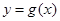 的图象过点
的图象过点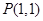 的切线方程;
的切线方程;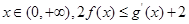 恒成立,求实数
恒成立,求实数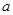 的取值范围。
的取值范围。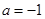 (2)x+y-2=0 (3) a≥-2
(2)x+y-2=0 (3) a≥-2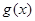 的两个极值点处导数为0 ,g’(x)=3x2+2ax-1带入
的两个极值点处导数为0 ,g’(x)=3x2+2ax-1带入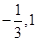 即可;
即可;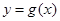 的图象过点
的图象过点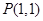 的切线方程,先求函数在点
的切线方程,先求函数在点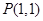 处的导数即斜率,在用点斜式求出方程;恒成立求实数
处的导数即斜率,在用点斜式求出方程;恒成立求实数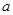 的取值范围时,一般分离参数,2a≥2lnx-3x-
的取值范围时,一般分离参数,2a≥2lnx-3x-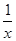 再在最值处成立即可。
再在最值处成立即可。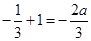
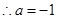
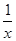
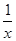
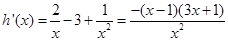


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:不详 题型:解答题
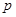 元(即税率为
元(即税率为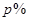 ),因此每年销量将减少
),因此每年销量将减少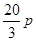 万件.
万件.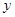 (万元),表示成
(万元),表示成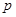 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;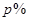 应怎样确定?
应怎样确定?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com