
分析 由已知数列递推式求得数列首项和公差,进一步求得数列通项和前n项和,代入λSn≥an-2016,分离参数λ,然后利用二次函数求得最值得答案.
解答 解:由an=$\sqrt{{S}_{2n-1}}$,得an2=S2n-1,
令n=1,n=2,
得$\left\{\begin{array}{l}{{{a}_{1}}^{2}={S}_{1}}\\{{{a}_{2}}^{2}={S}_{3}}\end{array}\right.$,即$\left\{\begin{array}{l}{{{a}_{1}}^{2}={a}_{1}}\\{({a}_{1}+d)^{2}=3{a}_{1}+3d}\end{array}\right.$,
∵an≠0,解得a1=1,d=2,
∴an=a1+(n-1)d=1+2(n-1)=2n-1,
${S}_{n}=n×1+\frac{n(n-1)}{2}×2={n}^{2}$.
由不等式λSn≥an-2016,得λn2≥2n-1-2016=2n-2017.
∴$λ≥\frac{2n-2017}{{n}^{2}}=\frac{2}{n}-\frac{2017}{{n}^{2}}$.
由二次函数的性质可知,当$\frac{1}{n}=\frac{1}{2017}$,即n=2017时,$(\frac{2}{n}-\frac{2017}{{n}^{2}})_{max}=\frac{2}{2017}-\frac{2017}{201{7}^{2}}=\frac{1}{2017}$.
∴实数λ的最小值为$\frac{1}{2017}$.
故答案为:$\frac{1}{2017}$.
点评 本题考查数列递推式,考查了等差数列通项公式的求法,训练了二次函数最值的求法,是中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-$\frac{5}{4}$) | C. | [-$\frac{5}{4}$,+∞) | D. | [-$\frac{5}{4}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
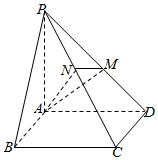 如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,PA=AD,点M、N分别在棱PD、PC上,且PC⊥平面AMN.
如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,PA=AD,点M、N分别在棱PD、PC上,且PC⊥平面AMN.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com