练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知等比数列前n项和为Sn，若S2=4，S4=16，则S6=（　　）
    A．52B．64C．-64D．-52

    分析 由等比数列的性质可得S2，S4-S2，S6-S4成等比数列，由题意求出公比，再由等比数列的通项公式分别求出S6的值．

    解答 解：由等比数列的性质可得S2，S4-S2，S6-S4成等比数列，
    又S2=4，S4=16，故S4-S2=12，所以公比为3，
    由等比数列可得：S6-S4=36，解得S6=52，
    故选：A．

    点评 本题考查等比数列的前n项和的性质，即片段和性质，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．正定中学教学处采用系统抽样方法，从学校高三年级全体800名学生中抽50名学生做学习状况问卷调查．现将800名学生从1到800进行编号，在1～16中随机抽取一个数，如果抽到的是7，则从41～56中应取的数是（　　）
    A．47B．48C．54D．55

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

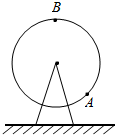    18．乐场有一个按逆时针方向旋转的大风车，如图所示．已知某人从点A处上风车，离地面的高度h（米）与它登上大风车后运行的时间t（分钟）满足函数关系h=12.5+10cos（$\frac{2π}{15}$t-$\frac{2π}{3}$），且5分钟后到达顶点B．
    （1）此人登上大风车开始运行时的点A距地面的高度为7.5；
    （2）点A转到点B所走过的弧度数为$\frac{2π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若正数a，b满足a+b=2，则$\frac{1}{a+1}$+$\frac{4}{b+1}$的最小值是（　　）
    A．1B．$\frac{9}{4}$C．9D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．函数f（x）=2x-log${\;}_{\frac{1}{2}}$（x-1），x∈（1，3]的值域是（-∞，7]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知等比数列{an}的前10项和为32，前20项和为56，则它的前30项和为74．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下列说法正确的是（　　）
    A．命题“若x2＜1，则-l≤x＜l”的逆否命题是“若x2≥1，则x＜-1或x≥l”
    B．命题“?x∈R，ex＞0”的否定是“?x∈R，ex≤0”
    C．“a＞0”是“函数f（x）=|（ax-1）x|在区间（-∞，0）上单调递减”的充要条件
    D．若“p∨q”为真命题，则p，q中至少有一个为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知函数$f（x）=\left\{\begin{array}{l}\frac{2x+1}{x^2}，x∈（{-∞，-\frac{1}{2}}）\\ ln（{x+1}），x∈[{-\frac{1}{2}，+∞}）\end{array}\right.$．g（x）=x2-4x-4．设b为实数，若存在实数a，使f（a）+g（b）=0，则b的取值范围是[-1，5]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若存在x0∈[1，3]，|x02-ax0+4|≤3x0，则实数a的取值范围是1≤a≤8．

    查看答案和解析>>

    同步练习册答案