
| A. | 命题“若x2<1,则-l≤x<l”的逆否命题是“若x2≥1,则x<-1或x≥l” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 若“p∨q”为真命题,则p,q中至少有一个为真命题 |
分析 直接写出命题的逆否命题判断A;写出全程命题的否定判断B;举反例说明C错误,由复合命题的真假判定判断D正确.
解答 解:命题“若x2<1,则-l≤x<l”的逆否命题是“若x<-1或≥1,则x2≥1”,A错误;
命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0”,B错误;
当a=0时,g(x)=(ax-1)x=-x,“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”;
∴“a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件错误;
若“p∨q”为真命题,则p,q中至少有一个为真命题,正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的否定与逆否命题,训练了充分必要条件的判定方法,是基础题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
| 全月应纳税所得额 | 税率(%) |
| 不超过1500元的部分 | 3 |
| 超过1500元至4500元的部分 | 10 |
| 超过4500元至9000元的部分 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
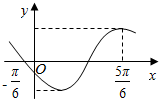 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | [一l,2] | C. | (0,2) | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
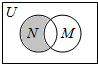 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com