
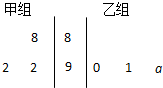
 以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示. 分析 (Ⅰ)直接由甲、乙两个小组的数学平均成绩相等列式求解a的值;
(Ⅱ)用枚举法列出所有可能的成绩结果,求出这两名同学中乙同学的成绩比甲同学的成绩好,然后由古典概率模型概率计算公式求概率.
(Ⅲ)由(Ⅰ)中求得的结果可得,当a=2,…,9时,乙组平均成绩超过甲组平均成绩,然后由古典概率模型概率计算公式求概率.
解答 解:(Ⅰ)由甲、乙两个小组的数学平均成绩相等,得$\frac{1}{3}$(88+92+92)=$\frac{1}{3}$[90+91+(90+a)],
解得a=1;
(Ⅱ)设“这两名同学中乙同学的成绩比甲同学的成绩好”为事件B,
当a=3时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有3×3=9种,它们是:
(88,90),(88,91),(88,93),(92,90),(92,91),(92,93),(92,90),
(92,91),(92,93).
∴事件B的结果有5种,它们是:(88,90),(88,91),(88,93),(92,93),(92,93).
∴P(B)=$\frac{5}{9}$.
(Ⅲ)设“乙组平均成绩超过甲组平均成绩”为事件A,
a的取值有:0,1,2,…,9共有10种可能.
由(Ⅰ)可知,当a=1时甲、乙两个小组的数学平均成绩相同,
∴当a=2,…,9时,乙组平均成绩超过甲组平均成绩,共有8种可能.
∴乙组平均成绩超过甲组平均成绩的概率P(A)=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题考查了茎叶图,考查了等可能事件的概率及古典概型概率计算公式,是中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪(0,+∞) | B. | (-∞,-1)∪[0,+∞) | C. | (-1,0] | D. | [-1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com