
分析 由配方法和二次函数的性质求出M,由指数函数的性质求出N,由新定义和并集的运算求出(M-N)、(N-M)和M⊕N.
解答 解:由y=x2-4x=(x-2)2-4得,y≥-4,
则M={y|y=x2-4x,x∈R}=[-4,+∞),
由y=2x>0得,y=-2x<0,则N={y|y=-2x,x∈R}=(-∞,0),
∵M-N={x|x∈M且x∉N},∴M-N=[0,+∞),N-M=(-∞,-4),
∵M⊕N=(M-N)∪(N-M),
∴M⊕N=[0,+∞)∪(-∞,-4),
故答案为:[0,+∞)∪(-∞,-4).
点评 本题考查了集合新定义和并集的运算,以及二次函数、指数函数的性质,属于基础题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:选择题
| A. | P=Q | B. | P⊆Q | C. | P?Q | D. | P∩Q=ϕ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
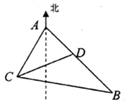 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 竞赛学科 | 数学 | 物理 | 化学 |
| 北大 | 6 | 4 | 2 |
| 清华 | 1 | 0 | 4 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{15}{34}$ | D. | $\frac{91}{136}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com