
分析 要证PA与PB垂直,即要求出PA的斜率和PB的斜率,把两个斜率相乘得到乘积为-1,所以以AB所在的直线为x轴,圆心为坐标原点建立平面直角坐标系,则得到A、B的坐标,设P(x,y),表示出PA与PB的斜率相乘,把P坐标代入圆的方程化简可得乘积为-1即可得证.
解答 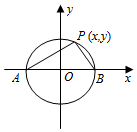 证明:将圆的直径AB所在的直线取为x轴,圆心作为原点,
证明:将圆的直径AB所在的直线取为x轴,圆心作为原点,
不妨设定圆的半径为1,于是圆的方程是x2+y2=1.
A、B的坐标是A(-1,0)、B(1,0).
设P(x,y)是圆上任一点,则有y2=1-x2.
∵PA的斜率为k1=$\frac{y}{x+1}$,PB的斜率为k2=$\frac{y}{x-1}$,
∴k1k2=$\frac{{y}^{2}}{{x}^{2}-1}$=$\frac{1-{x}^{2}}{{x}^{2}-1}$=-1
∴PA⊥PB,∠APB为直角.
即直径上的圆周角为直角,得证.
点评 此题为一道证明题,要求学生掌握两直线垂直的条件为斜率乘积为-1,会利用解析的方法证明数学问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{11}}{2}$ | B. | $\frac{\sqrt{14}}{2}$ | C. | $\sqrt{11}$ | D. | $\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
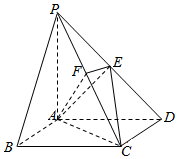 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
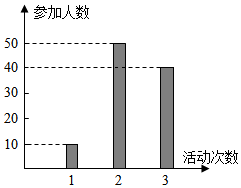 某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com