Question

如图，在正方体ABCD-A₁B₁C₁D₁中，E，F，M分别是BB₁，CC₁与AB的中点，
（1）求证：AE∥平面A₁DF；
（2）求证：A₁M⊥平面AED；
（3）正方体棱长为2，求三棱锥A₁-DEF的体积．

Answer 1

分析：（1）由正方体的几何特征，可证得EF∥AD，EF=AD，即或四边形AEFD为平行四DF边形，进而可得AE∥DF，结合线面平行的判定定理可得AE∥平面A₁DF；
（2）由正方体的几何特征可得AD⊥A₁M，由E，M分别是BB₁与AB的中点，可得△AA₁M≌△BAE，进而得到A₁M⊥AE，结合线面垂直的判定定理可得：A₁M⊥平面AED；
（3）三棱锥A₁-DEF的体积VA1-DEF=VA1-ADE=VD-A1AE，根据正方体棱长为2，代入棱锥体积公式，可得答案．

解答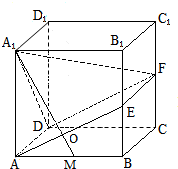：证明：（1）∵E，F分别是BB₁，CC₁的中点
∴EF∥BC，EF=BC
又∵AD∥BC，AD=BC
∴EF∥AD，EF=AD
∴四边形AEFD为平行四DF边形，
∴AE∥DF
∵AE?平面A₁DF，DF?平面A₁DF
∴AE∥平面A₁DF
（2）由正方体的几何特征可得AD⊥平面ABB₁A₁，
又∵A₁M?平面ABB₁A₁，
∴AD⊥A₁M
在正方形ABB₁A₁中，E，M分别是BB₁与AB的中点，
∴△AA₁M≌△BAE
∴∠BAE=∠AA₁M
∵∠BAE+∠AA₁O=90°
∴AA₁M+AA₁O=90°
∴A₁M⊥AE
∵AD∩AE=A，AD，AE?平面AED
∴A₁M⊥平面AED；
（3）∵正方体棱长为2，
∴三棱锥A₁-DEF的体积
VA1-DEF=VA1-ADE=VD-A1AE=

1

3

•S△A1AE•AD=

1

3

•

1

2

•2•2•2=

4

3

点评：本题考查的知识点是直线与平面垂直的判定，直线与平面平行的判定，熟练掌握空间线面关系的判定定理及几何特征是解答的关键．