
【题目】泰兴机械厂生产一种木材旋切机械,已知生产总利润c元与生产量x台之间的关系式为c(x)=-2x2+7 000x+600.
(1)求产量为1 000台的总利润与平均利润;
(2)求产量由1 000台提高到1 500台时,总利润的平均改变量;
(3)求c′(1 000)与c′(1 500),并说明它们的实际意义.
【答案】(1)5 000.6(元);(2)2 000(元);(3)见解析.
【解析】
(1)将x=1000代入函数可得总利润,总利润除以总数1000可得平均利润;
(2)计算![]() 即可得解;
即可得解;
(3)求导得c′(x),再分别计算c′(1 000)和c′(1 500),利用导数代表瞬时变化率可知为实际意义为生产一台多获利的钱数.
(1)产量为1 000台时的总利润为c(1 000)=-2×1 0002+7 000×1 000+600=5 000 600(元),平均利润为![]() =5 000.6(元).
=5 000.6(元).
(2)当产量由1 000台提高到1 500台时,总利润的平均改变量为![]() =
=![]() =2 000(元).
=2 000(元).
(3)∵c′(x)=(-2x2+7 000x+600)′=-4x+7 000,∴c′(1 000)=-4×1 000+7 000=3 000(元),
c′(1 500)=-4×1 500+7 000=1 000(元),
它们指的是当产量为1 000台时,生产一台机械可多获利3 000元;.
而当产量为1 500台时,生产一台机械可多获利1 000元.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=
,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED= ![]() ,EC=
,EC= ![]() .
. 
(Ⅰ)求sin∠BCE的值;
(Ⅱ)求CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海警基地码头O的正东方向40海里处有海礁界碑M,过点M且与OM成![]() (即北偏西
(即北偏西![]() )的直线l在在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东
)的直线l在在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东![]() 方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留. 基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.
方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留. 基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.
(1)如果O和A相距6海里,求可疑船被截获处的点P的轨迹;
(2)若要确保在领海内捕获可疑船(即P不能在公海上).则![]() 、
、![]() 之间的最大距离是多少海里?
之间的最大距离是多少海里?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求BD1与平面A1BC1所成角的正弦值.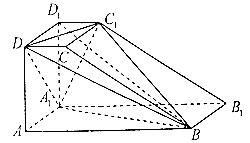
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C:![]() (a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=2c,过F2作x轴的垂线与双曲线在第一象限的交点为A,已知Q
(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=2c,过F2作x轴的垂线与双曲线在第一象限的交点为A,已知Q![]() ,|F2Q|>|F2A|,点P是双曲线C右支上的动点,且|PF1|+|AQ|>
,|F2Q|>|F2A|,点P是双曲线C右支上的动点,且|PF1|+|AQ|>![]() |F1F2|恒成立,则双曲线的离心率的取值范围是( )
|F1F2|恒成立,则双曲线的离心率的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品x件的总成本c(x)=120+![]() ,总成本的单位是元.
,总成本的单位是元.
(1)当x从200变到220时,总成本c关于产量x的平均变化率是多少?它代表什么实际意义?
(2)求c′(200),并解释它代表什么实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点
恒有两个不同的交点![]() 和
和![]() ,且
,且![]() (其中
(其中![]() 为坐标原点),求实数
为坐标原点),求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,![]() ,
,![]() 沿对角线将
沿对角线将![]() 折起,使点C移到
折起,使点C移到![]() 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.
(1)求证:![]() 平面ACD;
平面ACD;
![]() 求直线AB与平面
求直线AB与平面![]() D所成角的正弦值.
D所成角的正弦值.
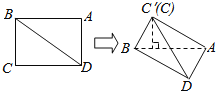
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com