以下有关线性回归分析的说法不正确的是( )A．通过最小二乘法得到的线性回归直线经过样本的中心B．用最小二乘法求回归直线方程.是寻求使最小的a,b的值C．在回归分析中.变量间的关系若是非确定性关系.但因变量也能由自变量唯一确定D．如果回归系数是负的.y的值随x的增大而减小题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

以下有关线性回归分析的说法不正确的是( )

A．通过最小二乘法得到的线性回归直线经过样本的中心

B．用最小二乘法求回归直线方程，是寻求使

最小的a,b的值

C．在回归分析中，变量间的关系若是非确定性关系，但因变量也能由自变量唯一确定

D．如果回归系数是负的，y的值随x的增大而减小

试题分析：根据题意，那么回归分析中，通过最小二乘法得到的线性回归直线经过样本的中心

成立对于用最小二乘法求回归直线方程，是寻求使

最小的a,b的值满足成立，对于如果回归系数是负的，y的值随x的增大而减小，类似于斜率为负数，成立排除法选C.具有相关关系的两个变量不一定是因果关系，因此选C.
点评：本题考查两个变量的线性相关，考查线性相关关系的意义，考查散点图和线性回归方程的作用，本题是一个概念辨析问题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：不详 题型：填空题

为了判断高中三年级学生是否选修文科与性别的关系，现随机抽取50名学生，得到如下2×2列联表：

	理科	文科
男	13	10
女	7	20

已知P(K²≥3.841)≈0.05，P(K²≥5.024)≈0.025.
根据表中数据，得到k＝

≈4.844.
则认为选修文科与性别有关系出错的可能性为________．

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

给出施化肥量（kg）对水稻产量（kg）影响的试验数据：

施化肥量x	15	20	25	30
水稻产量y	330	345	365	405

（1）试求出回归直线方程；
（2）请估计当施化肥量为10时，水稻产量为多少？
（已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125）

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

2012年元旦、春节前夕，各个物流公司都出现了爆仓现象，直接原因就是网上疯狂的购物．某商家针对人们在网上购物的态度在某城市进行了一次调查，共调查了124人，其中女性70人，男性54人．女性中有43人对网上购物持赞成态度，另外27人持反对态度；男性中有21人赞成网上购物，另外33人持反对态度．
(Ⅰ) 估计该地区对网上购物持赞成态度的比例；
(Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关；
附：表1

K²＝

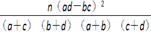
查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

对变量

与

,分别选择了4个不同的回归方程甲、乙、丙、丁,它们的相关系数

分别为:

，

. 其中拟合效果最好的是方程（）.

A．甲

B．乙

C．丙

D．丁

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

设有一个回归方程为y=2－3x，变量x增加1个单位时，则y平均( )

A．增加2个单位

B．减少2个单位

C．增加3个单位

D．减少3个单位

查看答案和解析>>

科目：高中数学 来源：不详 题型：单选题

对于一组数据

(

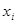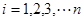)，如果将它们改变为

(

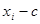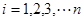)，其中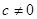

，下列结论正确的是( )

A．平均数与方差均不变	B．平均数变了，而方差保持不变
C．平均数不变，而方差变了	D．平均数与方差均发生了变化

查看答案和解析>>

科目：高中数学 来源：不详 题型：填空题

某种产品的广告费用支出