
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 是实数常数,
是实数常数,![]() ).
).
(1)若![]() ,函数
,函数![]() 的图象关于点
的图象关于点![]() 成中心对称,求
成中心对称,求![]() ,
,![]() 的值;
的值;
(2)若函数![]() 满足条件(1),且对任意
满足条件(1),且对任意![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 是奇函数,
是奇函数,![]() ,
,![]() ,且对任意
,且对任意![]() 时,不等式
时,不等式![]() 恒成立,求负实数
恒成立,求负实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)将![]() 化为
化为![]() ,类比
,类比![]() 的图象得对称中心
的图象得对称中心![]() ,对应相等可求得结果;(2)整理可得:
,对应相等可求得结果;(2)整理可得:![]() ;当
;当![]() 时符合题意;
时符合题意;![]() 时由单调性可知不合题意;当
时由单调性可知不合题意;当![]() 时,可知只需
时,可知只需![]() ,从而得到
,从而得到![]() 的范围;综合三种情况得到结果;(3)根据奇偶性和函数值可得:
的范围;综合三种情况得到结果;(3)根据奇偶性和函数值可得:![]() ,根据
,根据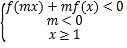 得到
得到![]() ,根据单调性求解出
,根据单调性求解出![]() 的最小值,则根据
的最小值,则根据![]() 求得结果.
求得结果.
(1)![]()
![]()
类比函数![]() 的图象,可知函数
的图象,可知函数![]() 的图象的对称中心是
的图象的对称中心是![]()
又![]() 函数
函数![]() 的图象的对称中心
的图象的对称中心![]()
![]()
(2)由(1)知,![]()
依据题意,对任意![]() ,恒有
,恒有![]() .
.
①当![]() 时,
时,![]() ,符合题意
,符合题意
②当![]() 时,对任意
时,对任意![]() ,则
,则![]()
恒有![]() ,不符合题意;
,不符合题意;
③当![]() 时,函数
时,函数![]() 在
在![]() 上是单调递减函数,且满足
上是单调递减函数,且满足![]()
因此,只需![]() 即可
即可
解得:![]()
综上所述,实数![]() 的范围
的范围![]()
(3)依据题设: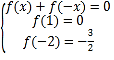 ,解得:
,解得: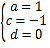
于是![]()
由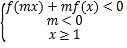 ,得
,得![]() ,
,
![]()
![]()
![]()
因此![]()
![]() 函数
函数![]() 在
在![]() 是增函数
是增函数
![]() .
.
![]() 所求负实数
所求负实数![]() 的取值范围
的取值范围![]()


科目:高中数学 来源: 题型:
【题目】定义:若存在常数![]() ,使得对定义域D内的任意两个不同的实数
,使得对定义域D内的任意两个不同的实数![]() ,均有:
,均有:![]() 成立,则称
成立,则称![]() 在D上满足利普希茨(Lipschitz)条件.
在D上满足利普希茨(Lipschitz)条件.
(1)试举出一个满足利普希茨(Lipschitz)条件的函数及常数![]() 的值,并加以验证;
的值,并加以验证;
(2)若函数![]() 在
在![]() 上满足利普希茨(Lipschitz)条件,求常数
上满足利普希茨(Lipschitz)条件,求常数![]() 的最小值;
的最小值;
(3)现有函数![]() ,请找出所有的一次函数
,请找出所有的一次函数![]() ,使得下列条件同时成立:
,使得下列条件同时成立:
①函数![]() 满足利普希茨(Lipschitz)条件;
满足利普希茨(Lipschitz)条件;
②方程![]() 的根
的根![]() 也是方程
也是方程![]() 的根,且
的根,且![]() ;
;
③方程![]() 在区间
在区间![]() 上有且仅有一解.
上有且仅有一解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有![]() 台大型机器,在
台大型机器,在![]() 个月中,
个月中,![]() 台机器至多出现
台机器至多出现![]() 次故障,且每台机器是否出现故障是相互独立的,出现故障时需
次故障,且每台机器是否出现故障是相互独立的,出现故障时需![]() 名工人进行维修.每台机器出现故障的概率为
名工人进行维修.每台机器出现故障的概率为![]() .已知
.已知![]() 名工人每月只有维修
名工人每月只有维修![]() 台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得
台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得![]() 万元的利润,否则将亏损
万元的利润,否则将亏损![]() 万元.该工厂每月需支付给每名维修工人
万元.该工厂每月需支付给每名维修工人![]() 万元的工资.
万元的工资.
(1)若每台机器在当月不出现故障或出现故障时有工人进行维修,则称工厂能正常运行.若该厂只有![]() 名维修工人,求工厂每月能正常运行的概率;
名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有![]() 名维修工人.
名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘![]() 名维修工人?
名维修工人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若函数
,若函数![]() 是增函数,则称函数
是增函数,则称函数![]() 具有性质A.
具有性质A.
![]() 若
若![]() ,求
,求![]() 的解析式,并判断
的解析式,并判断![]() 是否具有性质A;
是否具有性质A;
![]() 判断命题“减函数不具有性质A”是否真命题,并说明理由;
判断命题“减函数不具有性质A”是否真命题,并说明理由;
![]() 若函数
若函数![]() 具有性质A,求实数k的取值范围,并讨论此时函数
具有性质A,求实数k的取值范围,并讨论此时函数![]() 在区间
在区间![]() 上零点的个数.
上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)若![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的值;
的值;
(3)若![]() ,若当
,若当![]() 时,总有
时,总有![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有9个大小形状完全相同的球,球的编号分别为1,2,…,9,随机摸出两个球,则两个球的编号之和大于9的概率是______(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名企业为适应发展的需要,计划加大对研发的投入,据了解,该企业原有100名技术人员,年人均投入![]() 万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员
万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员![]() 名(
名(![]() 且
且![]() ),调整后研发人员的年人均投入增加
),调整后研发人员的年人均投入增加![]() %,技术人员的年人均投入调整为
%,技术人员的年人均投入调整为![]() 万元.
万元.
(1)要使这![]() 名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
(2)是否存在这样的实数![]() ,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出
,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由A,B,C,…等7人担任班级的7个班委.
(1)若正、副班长两职只能由A,B,C这三人中选两人担任,则有多少种分工方案?
(2)若正、副班长两职至少要选A,B,C这三人中的1人担任,有多少种分工方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com