
����Ŀ���μӺ�ˮ��ѧ��ѧѡ�ε�ͬѧ����ij��˾��һ�ֲ�Ʒ������۸����ͳ�ƣ��õ��������ݺ�ɢ��ͼ��
���� |
|
|
|
|
|
|
������ |
|
|
|
|
|
|
|
|
|
|
|
|
|
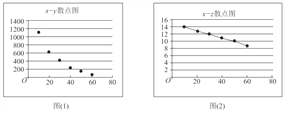
���ο����ݣ�![]()
![]() ��
��
��I������ɢ��ͼ�жϣ�![]() ��
��![]() ��
��![]() ��
��![]() ��һ�Ծ��н�ǿ����������ԣ������жϼ��ɣ�����˵�����ɣ���
��һ�Ծ��н�ǿ����������ԣ������жϼ��ɣ�����˵�����ɣ���
��II�����ݣ�I�����жϽ�������ݣ�����![]() ����
����![]() �Ļع鷽�̣������е�ϵ����������λ��Ч���֣���
�Ļع鷽�̣������е�ϵ����������λ��Ч���֣���
��III������Ϊ����Ԫ/![]() ʱ���������Ԥ��ֵ���
ʱ���������Ԥ��ֵ���
������һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��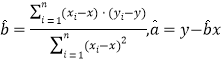 .
.
���𰸡���I����ɢ��ͼ��֪��![]() ��
��![]() ���н�ǿ�����������; ��II��
���н�ǿ�����������; ��II��![]() ; ��III����ֵΪ
; ��III����ֵΪ![]() Ԫ/
Ԫ/![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.
������������������Ƚ�����ɢ��ͼ���Է���![]() ��
��![]() ���н�ǿ����������ԣ����ñ����ṩ��
���н�ǿ����������ԣ����ñ����ṩ��![]() ��
��![]() �Ķ�Ӧֵ����
�Ķ�Ӧֵ����![]() ����������ṩ���ֳ�����
����������ṩ���ֳ�����![]() �ټ���
�ټ���![]() ���ó�
���ó�![]() ����
����![]() ���ó�
���ó�![]() ��������
��������![]() ����
����![]() ���ó�
���ó�![]() ����
����![]() �Ļع鷽�̣�ע�Ᵽ��С������ʾ�����������ҳ���ֵ.
�Ļع鷽�̣�ע�Ᵽ��С������ʾ�����������ҳ���ֵ.
���������
��I����ɢ��ͼ��֪��![]() ��
��![]() ���н�ǿ�����������.
���н�ǿ�����������.
��II������ã�![]() ��
��
![]() ��
��
 ��
��
��![]() ��
��
��![]() ��
��
�����Իع鷽��Ϊ![]() ��
��
��![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() .
.
��III����������Ϊ![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() �����
�����![]() .
.
�ɺ����ĵ����Կ�֪����![]() ʱ���������Ԥ��ֵ���
ʱ���������Ԥ��ֵ���
�ඨֵΪ![]() Ԫ/
Ԫ/![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���Sn=2n+1����n��N*����
��1��������{an}��ͨ��an��
��2����bn=nan+1 �� ������{bn}��ǰn���Tn��
��3����cn= ![]() ����֤��c1+c2+��+cn��
����֤��c1+c2+��+cn�� ![]() ����n��N*��
����n��N*��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() +
+ ![]() =1��a��b��0����������Ϊ
=1��a��b��0����������Ϊ ![]() ��������F����2��0����
��������F����2��0����
��1������ԲC�ķ��̣�
��2����ֱ��y=x+m����ԲC���ڲ�ͬ������A��B�����߶ε��е�M��Բx2+y2=1�ϣ���m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax3+cx��a��0��a��R��c��R������x=1ʱ��f��x��ȡ�ü�ֵ��2��
��1������f��x���Ľ���ʽ��
��2������f��x���ĵ�������ͼ���ֵ��
��3����������x1��x2��[��1��1]������ʽ|f��x1����f��x2��|��t���������ʵ��t����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �������ⳤ��Ϊ2��
�������ⳤ��Ϊ2�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣮
���е㣮

��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
��2�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex+2ax��aΪ��������ͼ����y�ύ�ڵ�A������y=f��x���ڵ�A��������б��Ϊ��1��
��1����a��ֵ������f��x���ļ�ֵ��
��2��֤������x��0ʱ��x2+1��ex ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
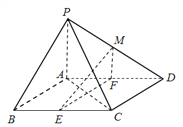
����Ŀ����ͼ��������![]() �У�����
�У�����![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ� ![]() ������
������![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() �ϣ�
�ϣ�
������֤�� ![]() ƽ��
ƽ��![]() ��
��
�������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽǺ�ֱ��
���ɵĽǺ�ֱ��![]() ��ƽ��
��ƽ��![]() ���ɵĽ���ȣ���
���ɵĽ���ȣ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() .
.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ������
������![]() ����������㣬��
����������㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ�У�ԲC�ķ���Ϊ��=2acos�ȣ�a��0�����Լ���Ϊ����ԭ�㣬����Ϊx�������Ὠ��ƽ��ֱ������ϵ����ֱ��l�IJ�������Ϊ ![]() ��tΪ��������
��t��������
��1����ԲC�ı����̺�ֱ��l����ͨ���̣�
��2����ֱ��l��ԲC���й����㣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com