
| x | 3 | 4 | 5 | 6 | 7 |
| y | 2.5 | 3 | 3.5 | 4 | 5.5 |
分析 (1)把所给的五对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.
(2)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(3)根据上一问所求的线性回归方程,把x=100代入线性回归方程,即可估计生产100吨甲产品的生产能耗.
解答 解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.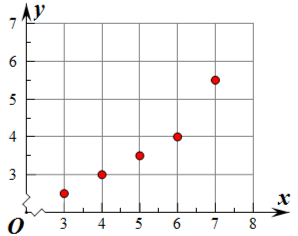
(2)
| x | 3 | 4 | 5 | 6 | 7 |
| y | 2.5 | 3 | 3.5 | 4 | 5.5 |
| xy | 7.5 | 12 | 17.5 | 24 | 38.5 |
| X2 | 9 | 16 | 25 | 36 | 49 |
点评 本题考查线性回归方程,两个变量之间的关系,除了函数关系,还存在相关关系,通过建立回归直线方程,就可以根据其部分观测值,获得对这两个变量之间整体关系的了解,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 23 | C. | 32 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1±\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}±1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1<x<2} | C. | {x|x≥2或x≤-1} | D. | {x|x>2或x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com