【题目】若函数
的极大值为6，极小值为2，则
的单调递减区间是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
根据函数f（x）=x3﹣3ax+b（a＞0）的极大值为6，极小值为2，求导f′（x）=0，求得该函数的极值点x1，x2，并判断是极大值点x1，还是极小值点x2，代入f（x1）=6，f（x2）=2，解方程组可求得a，b的值，再由f′（x）＜0即可得到．
令f′（x）=3x2﹣3a=0，得x=±
，
令f′（x）＞0得x＞或x＜﹣；令f′（x）＜0得﹣＜x＜．
即x=﹣取极大，x=取极小．
∵函数f（x）=x3﹣3ax+b（a＞0）的极大值为6，极小值为2，
∴f（）=2，f（﹣）=6，
即a﹣3a+b=2且﹣a+3a+b=6，
得a=1，b=4，
则f′（x）=3x2﹣3，由f′（x）＜0得﹣1＜x＜1．
则减区间为（﹣1，1）．
故选：Ａ．
科目：高中数学 来源： 题型：
【题目】某商场销售某种商品的经验表明，该商品每日的销售量
(单位：千克)与销售价格
(单位：元/千克)满足关系式
，其中
为常数.已知销售价格为5元/千克时，每日可售出该商品13千克.
（1）求
的值；
（2）若该商品的成本为3元/千克，试确定销售价格的值，使商场每日销售该商品所获得的利润最大，并求出最大利润.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两个焦点分别为
和
，过点
的直线与椭圆相交与
两点，且
.
（1）求椭圆的离心率；
（2）求直线
的斜率；
（3）设点
与点
关于坐标原点对称，直线
上有一点
在
的外接圆上，且
，求椭圆方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】抛掷一颗质地均匀的骰子，有如下随机事件：
=“点数为i”，其中
；
=“点数不大于2”，
=“点数大于2”，
=“点数大于4”；E=“点数为奇数”，F=“点数为偶数”.判断下列结论是否正确.
（1）
与
互斥；（2），
为对立事件；（3）
；（4）
；（5）
，
；
（6）
；（7）
；（8）E，F为对立事件；（9）
；（10）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年来，随着汽车消费水平的提高，二手车流通行业得到迅猛发展.某汽车交易市场对2017 年成交的二手车的交易前的使用时间（以下简称“使用时间”）进行统计，得到频率分布直方图如图1.在图1对使用时间的分组中，将使用时间落入各组的频率视为概率.
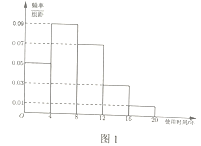
（1）记“在2017年成交的二手车中随机选取一辆，该车的使用年限在
”，为事件
，试估计的概率；
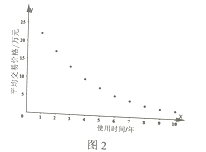
（2）根据该汽车交易市场的历史资料，得到散点图如图，其中
(单位：年)表示二手车的使用时间，
（单位：万元)表示相应的二手车的平均交易价格.
由散点图判断，可采用
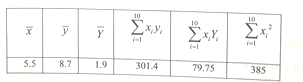
作为二手车平均交易价格关于其使用年限的回归方程，相关数据如下表(表中
)：
①根据回归方程类型及表中数据，建立关于的回归方程；
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格
的佣金，对使用时间8年以上（不含 8年)的二手车收取成交价格
的佣金. 在图1对使用时间的分组中，以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据，计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注：①对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
，
；
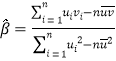②参考数据：
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与“不合格”，两部分考核都是“合格”，则该课程考核“合格”，若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7，在实验考核中合格的概率分别为0.8,0.7,0.9，所有考核是否合格相互之间没有影响．
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率；
(2)求这三个人该课程考核都合格的概率(结果保留三位小数)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系．设曲线C的参数方程为
(θ为参数)，直线l的极坐标方程为ρcos
＝2
.
(1)写出曲线C的普通方程和直线l的直角坐标方程；
(2)求曲线C上的点到直线l的最大距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
