
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,过点
,过点![]() 的直线与椭圆相交与
的直线与椭圆相交与![]() 两点,且
两点,且![]() .
.
(1)求椭圆的离心率;
(2)求直线![]() 的斜率;
的斜率;
(3)设点![]() 与点
与点![]() 关于坐标原点对称,直线
关于坐标原点对称,直线![]() 上有一点
上有一点![]() 在
在![]() 的外接圆上,且
的外接圆上,且![]() ,求椭圆方程.
,求椭圆方程.
【答案】(1)![]() .
.
(2)![]() .
.
(3)![]() .
.
【解析】
(1)由![]() ,
,![]() ,得
,得![]() ,得到
,得到![]() 的关系式,由此能求出离心率;(2)将椭圆的方程为写为
的关系式,由此能求出离心率;(2)将椭圆的方程为写为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,联立方程组,由此利用根的判别式、韦达定理,结合已知条件能求出直线
,联立方程组,由此利用根的判别式、韦达定理,结合已知条件能求出直线![]() 的斜率;(3)求出
的斜率;(3)求出![]() ,
,![]() ,取
,取![]() ,得
,得![]() ,推导出外接圆的方程,与直线
,推导出外接圆的方程,与直线![]() 的方程联立解出
的方程联立解出![]() ,得,再由
,得,再由![]() ,解得
,解得![]() ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(1)由![]() 且
且![]() ,得
,得![]() ,从而
,从而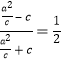
整理,得![]() ,故离心率
,故离心率![]() .
.
(2)由(1)得![]() ,所以椭圆的方程可写为
,所以椭圆的方程可写为![]()
设直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由已知设![]() ,则它们的坐标满足方程组
,则它们的坐标满足方程组![]()
消去![]() 整理,得
整理,得![]() .
.
依题意,![]() ,得
,得![]() .
.
而![]() ①
①
![]() ②
②
由题设知,点![]() 为线段
为线段![]() 的中点,所以
的中点,所以
![]() ③
③
联立①③解得![]()
将![]()
![]() 代入②中,解得
代入②中,解得![]() .
.
(3)由(2)可知![]() .
.
不妨取![]() ,得
,得![]() ,由已知得
,由已知得![]() .
.
线段![]() 的垂直平分线
的垂直平分线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点
轴的交点![]() 是
是![]() 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为![]() .
.
直线![]() 的方程为
的方程为![]() ,于是点
,于是点![]() 的坐标满足方程组
的坐标满足方程组
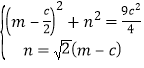 ,由
,由![]() ,解得
,解得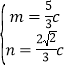
由![]() 解得
解得![]()
故椭圆方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校初中部共120名教师,高中部共180名教师,其性别比例如图所示,已知按分层抽样方法得到的工会代表中,高中部女教师有6人,则工会代表中男教师的总人数为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() ,则
,则![]() 解集为
解集为![]() ;
;
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)![]() 为常数,若对任意的
为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称.
对称.
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在试验E“连续抛掷一枚骰子2次,观察每次掷出的点数”中,事件A表示随机事件“第一次掷出的点数为1”,事件![]() 表示随机事件“第一次掷出的点数为1,第二次掷出的点数为j,事件B表示随机事件“2次掷出的点数之和为6”,事件C表示随机事件“第二次掷出的点数比第一次的大3”,
表示随机事件“第一次掷出的点数为1,第二次掷出的点数为j,事件B表示随机事件“2次掷出的点数之和为6”,事件C表示随机事件“第二次掷出的点数比第一次的大3”,
(1)试用样本点表示事件![]() 与
与![]() ;
;
(2)试判断事件A与B,A与C,B与C是否为互斥事件;
(3)试用事件![]() 表示随机事件A.
表示随机事件A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)把![]() 本不同的书分给
本不同的书分给![]() 位学生,每人至少一本,有多少种方法?
位学生,每人至少一本,有多少种方法?
(2)由![]() 这
这![]() 个数字组成没有重复数字的四位偶数由多少个?
个数字组成没有重复数字的四位偶数由多少个?
(3)某旅行社有导游![]() 人,其中
人,其中![]() 人只会英语,
人只会英语,![]() 人只会日语,其余
人只会日语,其余![]() 人既会英语,也会日语,现从中选
人既会英语,也会日语,现从中选![]() 人,其中
人,其中![]() 人进行英语导游,另外
人进行英语导游,另外![]() 人进行日语导游,则不同的选择方法有多少种?
人进行日语导游,则不同的选择方法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com