
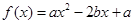 (
(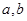
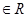 )
)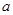 从集合
从集合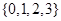 中任取一个元素,
中任取一个元素, 从集合
从集合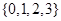 中任取一个元素,
中任取一个元素,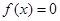 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;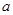 从区间
从区间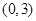 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数
中任取一个数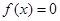 没有实根的概率.
没有实根的概率.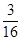 (2)
(2)
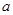 取集合
取集合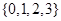 中任一个元素,
中任一个元素, 取集合{0,1,2,3}中任一个元素
取集合{0,1,2,3}中任一个元素 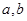 取值的情况是:
取值的情况是: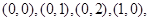


 ,(0,3),(1,3),(2,3),(3,3)其中第一个数表示
,(0,3),(1,3),(2,3),(3,3)其中第一个数表示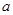 的取值,第二个数表示
的取值,第二个数表示 的取值.
的取值.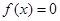 恰有两个不相等的实根”为事件
恰有两个不相等的实根”为事件 3分
3分 时,方程
时,方程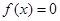 恰有两个不相等实根的充要条件为b>
恰有两个不相等实根的充要条件为b>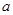 且
且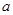 不等于零
不等于零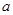 时,
时,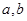 取值的情况有(1,2),(1,3),(2,3),
取值的情况有(1,2),(1,3),(2,3), 包含的基本事件数为3, 5分
包含的基本事件数为3, 5分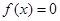 恰有两个不相等实根的概率
恰有两个不相等实根的概率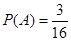 7分
7分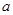 从区间
从区间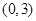 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数
中任取一个数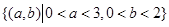
 9分
9分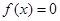 没有实根”为事件B, 10分
没有实根”为事件B, 10分

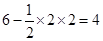 12分
12分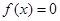 没有实根的概率
没有实根的概率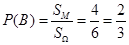 15分
15分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
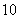 个编号为
个编号为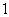 、
、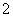 、
、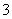 的球,
的球,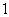 号球有
号球有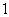 个,
个,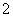 号球有
号球有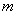 个,
个, 号球有
号球有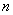 个.从袋中依次摸出
个.从袋中依次摸出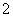 个球,已知在第一次摸出
个球,已知在第一次摸出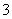 号球的前提下,再摸出一个
号球的前提下,再摸出一个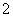 号球的概率是
号球的概率是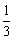 .
.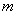 、
、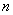 的值;
的值;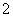 个球,记得到小球的编号数之和为
个球,记得到小球的编号数之和为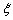 ,求随机变量
,求随机变量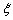 的分布列和数学期望
的分布列和数学期望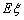 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
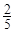 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时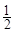 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )A.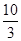 | B.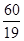 | C.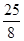 | D.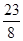 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
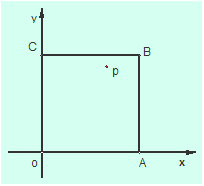
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
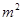 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com