
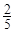 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时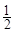 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )A.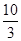 | B.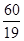 | C.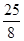 | D.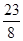 |
科目:高中数学 来源:不详 题型:解答题
 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记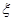 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求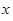 的分布列及期望。
的分布列及期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
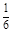 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
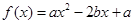 (
(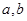
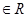 )
)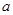 从集合
从集合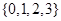 中任取一个元素,
中任取一个元素, 从集合
从集合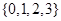 中任取一个元素,
中任取一个元素,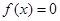 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;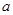 从区间
从区间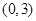 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数
中任取一个数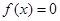 没有实根的概率.
没有实根的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com