
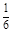 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料. 计算高手系列答案
计算高手系列答案科目:高中数学 来源:不详 题型:解答题
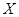 ,求
,求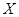 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在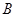 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在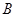 处投;方案2:都在
处投;方案2:都在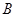 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为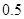 ,在
,在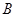 处投篮的命中率为
处投篮的命中率为 .
. 的分布列和数学期望
的分布列和数学期望 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
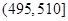 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.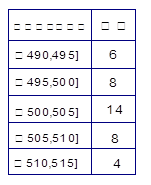
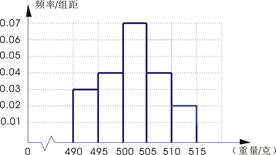
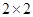 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 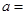 | 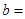 | |
| 不合格品 | 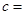 | 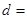 | |
| 合 计 | | | 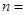 |
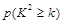 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
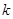 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
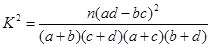 ,其中
,其中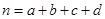 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
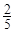 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时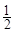 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )A.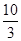 | B.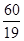 | C.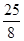 | D.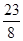 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
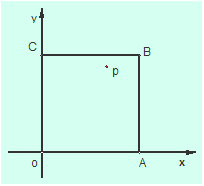
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
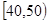 ,
,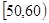 …
…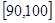 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: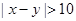 ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com