
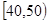 ,
,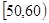 …
…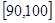 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: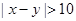 ”的概率.
”的概率.
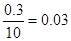 ;
;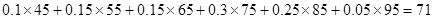
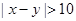 ”的概率是
”的概率是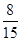 .
.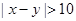 ”包含的基本结构的个数,再利用古典概型概率计算公式计算其概率即可.
”包含的基本结构的个数,再利用古典概型概率计算公式计算其概率即可.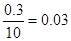 ,对应图形如图所示: 4分
,对应图形如图所示: 4分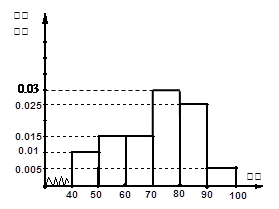
 考试的及格率即60分及以上的频率
考试的及格率即60分及以上的频率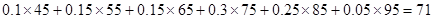 ……8分
……8分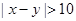 ”为事件A
”为事件A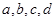 ,90~100分数段的2人的成绩分别为
,90~100分数段的2人的成绩分别为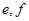 ,则从中选两人,其成绩组合
,则从中选两人,其成绩组合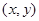 的所有情况有:
的所有情况有: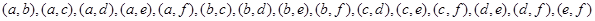 ,共15种,且每种情况的出现均等可能.若这2人成绩要满足“
,共15种,且每种情况的出现均等可能.若这2人成绩要满足“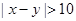 ”,则要求一人选自40~50分数段,另一个选自90~100分数段,有如下情况:
”,则要求一人选自40~50分数段,另一个选自90~100分数段,有如下情况: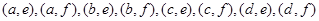 ,共8种,所以由古典概型概率公式有
,共8种,所以由古典概型概率公式有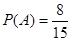 ,即所取2人的成绩满足“
,即所取2人的成绩满足“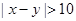 ”的概率是
”的概率是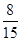 .14分
.14分

科目:高中数学 来源:不详 题型:解答题
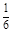 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | Z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com