
 ; (2)一等奖可设价值为310 元的奖品。
; (2)一等奖可设价值为310 元的奖品。 ,
,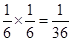 ; …………2分
; …………2分 ;
; ; …………6分
; …………6分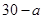 ,
, ,0,
,0, ,……7分
,……7分| ξ | 30-a | -70 | 0 | 30 |
| p |  |  |  |  |
 ; …………11分
; …………11分

科目:高中数学 来源:不详 题型:解答题
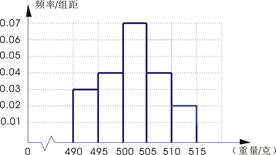
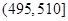 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.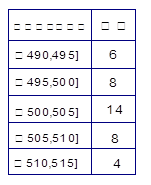
 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 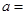 | 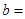 | |
| 不合格品 | 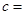 | 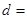 | |
| 合 计 | | | 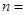 |
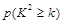 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
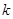 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
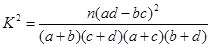 ,其中
,其中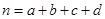 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
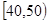 ,
,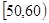 …
…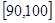 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: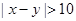 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 处,准备开车到单位
处,准备开车到单位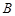 处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如
处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如 算作两个路段:路段
算作两个路段:路段 发生堵车事件的概率为
发生堵车事件的概率为 ,路段
,路段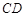 发生堵车事件的概率为
发生堵车事件的概率为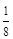 ).
).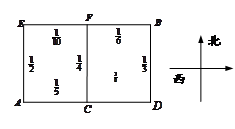
 到
到 的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小; 中遇到堵车次数为随机变量
中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
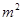 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com