
 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在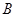 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在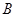 处投;方案2:都在
处投;方案2:都在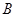 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为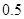 ,在
,在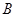 处投篮的命中率为
处投篮的命中率为 .
. 的分布列和数学期望
的分布列和数学期望 ;
; 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:不详 题型:解答题
 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分. 的分布列及其数学期望E(
的分布列及其数学期望E( );
);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
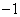 ,先从中任取三张卡片,将卡片上的数字相加,设数字和为
,先从中任取三张卡片,将卡片上的数字相加,设数字和为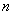 ,当
,当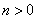 时,奖励奖金
时,奖励奖金 元;当
元;当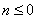 时,无奖励.
时,无奖励.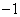 的概率.
的概率.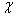 为奖金金额,求
为奖金金额,求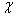 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
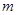 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为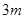 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为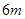 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是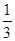 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
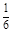 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com