
| A. | $\frac{13}{5}$ | B. | $-\frac{13}{5}$ | C. | $\frac{{13\sqrt{53}}}{53}$ | D. | $-\frac{{13\sqrt{53}}}{53}$ |
分析 根据题意,结合向量的物理意义,计算可得粒子B相对粒子A的位移是$\overrightarrow s$=$\overline{{S}_{B}}$-$\overline{{S}_{A}}$,进而结合数量积的运算计算$\overrightarrow s$在$\overrightarrow{s_B}$的投影$\frac{\overrightarrow{S}•\overrightarrow{{S}_{B}}}{|\overrightarrow{{S}_{B}}|}$,即可得答案.
解答 解:根据题意,两个粒子A,B的位移分别为$\overrightarrow{s_A}=({2,10}),\overrightarrow{s_B}=({4,3})$,
则粒子B相对粒子A的位移是$\overrightarrow s$=$\overline{{S}_{B}}$-$\overline{{S}_{A}}$=(2,-7),
$\overrightarrow s$在$\overrightarrow{s_B}$的投影为$\frac{\overrightarrow{S}•\overrightarrow{{S}_{B}}}{|\overrightarrow{{S}_{B}}|}$=$\frac{2×4+3×(-7)}{\sqrt{{4}^{2}+{3}^{2}}}$=-$\frac{13}{5}$;
故选:B.
点评 本题考查向量的数量积的应用,涉及向量的坐标运算,关键是理解向量的概念,将物理问题转化为数学问题.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°
如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
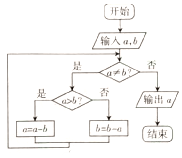 秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( )
秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( )| A. | 30 | B. | 18 | C. | 5 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com