
分析 (Ⅰ)利用立方和公式、结合配方法,即可证明;
(Ⅱ)若至少存在一个实数x,使得|x-a|+|x-b|≤5成立,则|a-b|≤5,由此求实数2a+3b的取值范围.
解答 (Ⅰ)证明:a3+b3=(a+b)(a2-ab+b2)=a2-a(1-a)+(1-a)2=$3(a-\frac{1}{2})^{2}+\frac{1}{4}$≥$\frac{1}{4}$;
(Ⅱ)解:|x-a|+|x-b|≥|x-a-x+b|=|a-b|,至少存在一个实数x,使得|x-a|+|x-b|≤5成立,则|a-b|≤5,
∵a+b=1,∴b=1-a,
∴|a-(1-a)|≤5,
∴-2≤a≤3,
∴2a+3b=3-a∈[0,5].
点评 本题考查不等式的证明,考查绝对值不等式的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{5}$ | B. | $-\frac{13}{5}$ | C. | $\frac{{13\sqrt{53}}}{53}$ | D. | $-\frac{{13\sqrt{53}}}{53}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
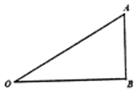 如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.
如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | [1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1]∪(0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com