
分析 (Ⅰ)利用4Sn=an2+2an-3,再写一式,两式相减,利用当n≥7时,an>0,即可得出{an}成等差数列;
(Ⅱ)确定首项,公比,即可求{an}的前7项和S7.
解答 (Ⅰ)证明:由4Sn=an2+2an-3,4Sn+1=an+12+2an+1-3,
两式相减整理得,(an+1+an)(an+1-an-2)=0…(4分)
当n≥7时,an>0,∴an+1-an=2,
∴当n≥7时,{an}成等差数列.
(Ⅱ)解:由4S1=a12+2a1-3,得a1=3或a1=-1
又a1,a2,a3,a4,…,a7成等比数列,
∴an+1+an=0(n≤6),q=-1,
而a7>0,∴a1>0,从而a1=3.
∴S7=3-3+3-3+3-3+3=3.….(14分)
点评 本题考查等差数列的证明,考查数列的求和,考查数列递推式,考查学生分析解决问题的能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
 如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°
如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用时间(单位:天) | 10:20 | 21:30 | 31:40 | 41:50 | 51:60 |
| 个数 | 10 | 40 | 80 | 50 | 20 |
| A. | $\frac{13}{16}$ | B. | $\frac{27}{64}$ | C. | $\frac{25}{32}$ | D. | $\frac{27}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
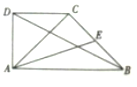 如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.
如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com