Question

已知集合P={x|5x-a≤0}，Q={x|6x-b＞0}，a，b∈N，且P∩Q∩N={2，3，4}，则整数对（a，b）的个数为________．

Answer 1

20
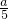
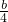
分析：由不等式的解法，可得A、B，进而由P∩Q∩N={2，3，4}，可得 、的取值范围，进而由a，b∈N，可得a、b的值，进而可得答案．
解答：由不等式的解法，可得P={x|5x-a≤0}={x|}，
Q={x|6x-b＞0}={x|x}，
又有P∩Q∩N={2，3，4}，
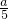
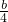
则有4≤＜5，1≤＜2，
解可得，20≤a＜25，4≤b＜8，
又有a，b∈N，
则a=20、21、22、23、24，b=4、5、6、7，
则整数对（a，b）的个数为20个．
故答案为：20．
点评：本题考查集合的交集运算，有一定的难度，解题时，要注意P∩Q∩N={2，3，4}，这一条件的运用．